XYZ is a colorspace like RGB. The acronym of XYZ doesn't stand for anything, unlike RGB - abbreviation of Red, Green, Blue - or CMYK - abbreviation of Cyan, Magenta, Yellow, Black/Key.
Why the choice of XYZ
Why don't we use the RGB directly ?
We will see why in this chapter.
In the chapter history of digital cinema, I had mentioned the SMPTE DC28 Color group, which worked on all aspects of colorimetry. They had many discussions about various color space. A Parametric RGB with metadata was mentioned but it was dismissed because if the metadata were misinterpreted by the projector, the colors will be altered.
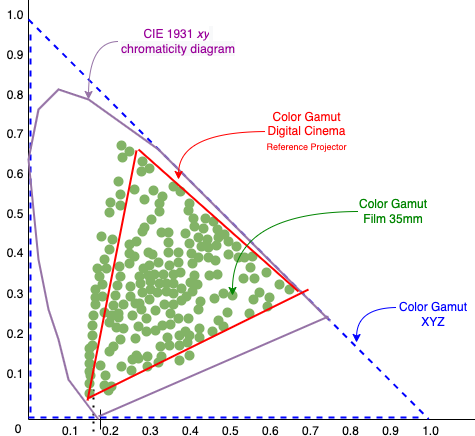
In the end, the group opted for the XYZ color space because of its wide color gamut, and because it has existed since decades (since 1931), this color space is already used in other fields, is future-proof and covers the entire color space (even outside the visible spectrum). It is so wide that it can cover both the digital cinema color space and the 35mm color space :

The XYZ color space is independent of both metadata and specific projection equipment. Its luminance is encoded in the Y value, and at last, its integration into various workflows won't be very difficult (all you need is to linearize the RGB input, apply its own 3x3 conversion matrix and to encode the gamma).
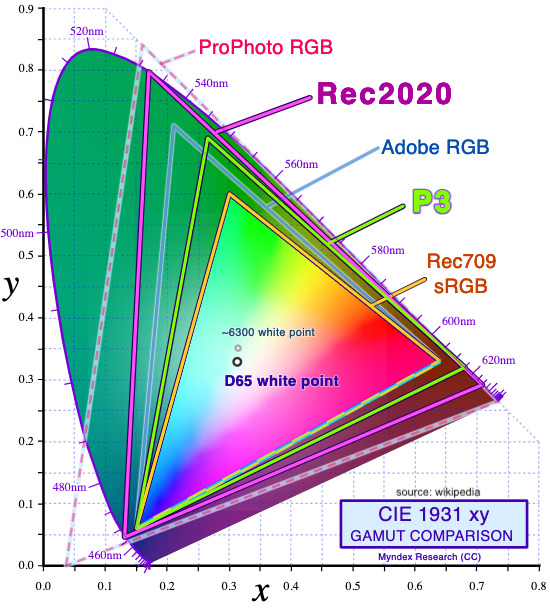
The XYZ color space has a wide color gamut (in blue), it encompasses the whole visible spectrum (in purple) and therefore covers almost 1 all of colorspace available. We can easily switch to more limited colorspace without much trouble.
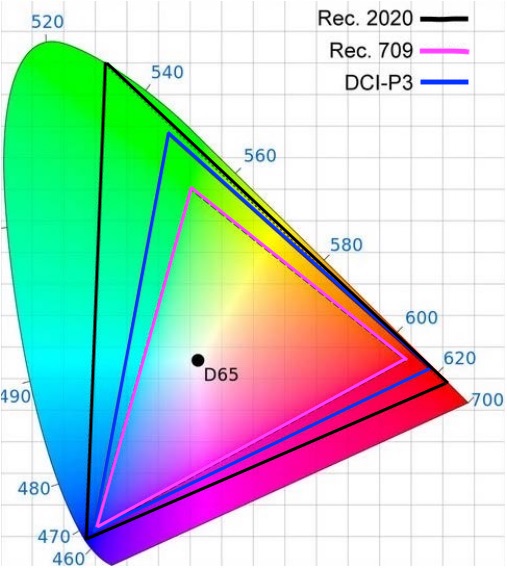
The other advantage is its independence from another colorspace : while the image is in XYZ, the projector uses the DCI-P3 colorspace (see the paragraph "DCI-P3 colorspace below). The DCI-P3 is a wider colorspace than sRGB-Rec709 colorspace, but not as wide as the Rec2020 colorspace. If, in the future, the equipment manufacturers might change the output colorspace, such as to Rec2020 or a new DCI-P2-20xx, we don't need to re-encode the entire image, and therefore, we don't need to regenerate the entire DCP. That's the advantage of using the XYZ colorspace.
For more information about the history of SMPTE, the choice of XYZ colorspace, the experimentation and mathematical equations, I suggest the book Color and Mastering for Digital Cinema by Glenn Kennel who dedicates a specific chapter for all of these aspects.
In the 1920s, in order to create a stable definition of RGB colorspace, two experimentations were initiated .. with the means of the time : a bunch of human observers and the naked-eyes tests. These works led to the publication of a paper defining the premises of the CIE RGB :

However, the CIE RGB colorspace has several problems, especially with some negative values. For example, several red values are below the zero :
The Commission Internationale de l'Eclairage initiated a new colorspace derived from CIE RGB : CIE XYZ colorspace. In 1931, the XYZ colorspace was standardized under the name "CIE XYZ 1931" :
For the curves
The X, Y, and Z primitives don't have physical reality 3, these are just mathematical concepts, three virtual primary colors, where the Y value represents the luminance component, and all values are always positive 4, 5, 6.
Through the years, several improvements have been applied to the XYZ colorspace. To avoid using outdated technical methods such as those used in 1931 (bunch of people, rudimentary tools), the new XYZ colorspaces were based on more stable foundations and were named CIE XYZ 2006 and CIE XYZ 2015.
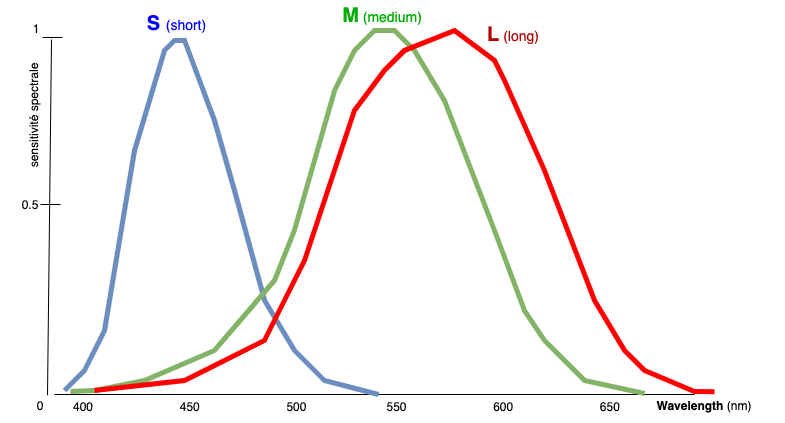
For example, now, we use a new type of color space called LMS (for Long, Medium, and Short wavelengths), which represents how the light is absorbed by the cones in the retina of the eye. Through various experiments, three curves have been obtained, as shown in the following diagram (LMS fonctions). Based on these LMS curves, we can now generate the CIE XYZ Color Matching Functions (CMF) and their corresponding
|
↔ |

|
| LMS fonctions | CIE XYZ Color Matching Functions |
For our above LMS curves, L, M, and S represent the different types of photoreceptor in the eye. Thus, the S curve (blue) is associated with "blue-purple" colors, the M curve (green) is associated with green colors, and the L curve (red) is associated with red-yellow colors.
The advantage of using LMS is that it allows us to generate the CIE RGB and the CIE XYZ colorspace through simple linear transformations using matrices
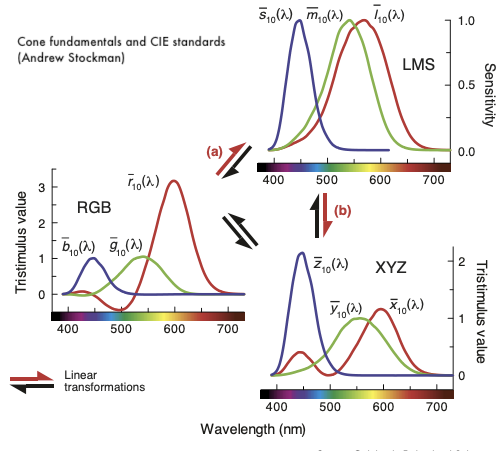
An example of a conversion from LMS to XYZ 2006;2015 using a simple matrix (marked
x = ( 1.94735469 -1.41445123 0.36476327 ) * ( l )
y = ( 0.68990272 0.34832189 0 ) * ( m )
z = ( 0 0 1.93485343 ) * ( s )
These functions and matrices are evolutions of the original CIE XYZ 1931. However, the XYZ used in DCP is still based on the original CIE XYZ 1931. In the future, it might be a CIE XYZ 2005;2016, but not yet.
For more information about the history of XYZ, you could refer to these two websites :
A brief aside about the DCI-P3 colorspace which you might see in other chapters.
The RGB DCI-P3 is a wider colorspace than sRGB-Rec709 colorspace (but not as wide as the Rec2020 colorspace).
DCI-P3 is used both for theatrical projection and for the display in color grading software.
A summary :
DCI-P3 is the name of a specific RGB for theatrical projection or postproduction workflow in digital cinema.
DCI-P3 is a colorspace used on theatrical projection and color grading software.
The gamma output of RGB DCI-P3 is Gamma 2.6 [SMPTE-431-2]
Depending on the input source, you may work on various colorspace, such as sRGB or RGB DCI-P3. If you have RGB images, you must pay attention to which ones use sRGB and which ones use RGB DCI-P3. Advice from a guy who lost too much time on an SRGB input misinterpreted as DCI-P3 :)
If you get mixed up, conversion process won't be the same, the matrices will differ, and the input gamma too. (sRGB uses a gamma 2.2, while DCI-P3 uses a gamma 2.6)
The XYZ conversion matrices used in the examples in this chapter are based on RGB DCI-P3.
You may see this format a lot in the output of postproduction software
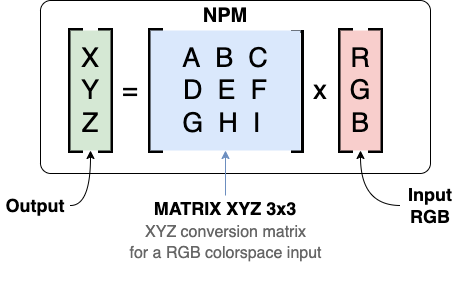
To convert to XYZ, you must apply a matrix transformation to each value from the source :

Behind these symbols, there is only a series of additions and multiplications between the NPM "RGB-to-XYZ" matrix and the input source (here, an RGB)
The NPM - abbreviation for Normalized Primary Matrix - is simply a term used to indicate that we are dealing with an interchangeable matrix depending on the input source.
Thus, if you have an sRGB input, you will have a matrix with specific values which allow conversion of sRGB values to XYZ values (and vice versa). If you have a DCI-P3 input, you will have another matrix, and so on for each colorspace.
This normalized primary matrix is an 3x3 matrix 8 which will be multiplied by the input values to give its XYZ output :
A simplified form of this computation (almost) :
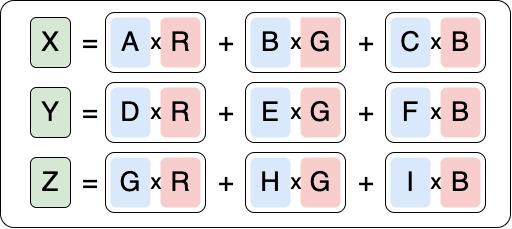
Thus, for example, if we have an XYZ matrix (NPM) like this :
[ 1, 3, 4 ]
[ 6, 1, 2 ]
[ 8, 9, 5 ]
and an input like this :
[ 22, 33, 44 ]
Our matrix computation will be :
( 1 * 22 ) + ( 3 * 33 ) + ( 4 * 44 )
( 6 * 22 ) + ( 1 * 33 ) + ( 2 * 44 )
( 8 * 22 ) + ( 9 * 33 ) + ( 5 * 44 )
From this point, we can apply any matrix to any input.
The XYZ conversion involves taking each source value and applying a specific matrix based on the input colorspace (sRGB, DCI-P3, ...) : the output will be new values in XYZ colorspace.
There are various conversion matrices to XYZ colorspace (see the paragraph Matrix Museum) because for each existing input colorspace, there is a corresponding conversion matrix. Here, we use two matrixes : one for RGB DCI-P3 and one for sRGB/Rec709 9 :
The official matrix DCI-P3 → XYZ defined in the SMPTE 431-2 - Reference Projector and Environment :
| R x | G x | B x | ||||
|---|---|---|---|---|---|---|
| X | = | 0.4451698156 | + | 0.2771344092 | + | 0.1722826698 |
| Y | = | 0.2094916779 | + | 0.7215952542 | + | 0.0689130679 |
| Z | = | 0.0000000000 | + | 0.0470605601 | + | 0.9073553944 |
The official matrix sRGB/Rec709 → XYZ defined in the SMPTE RP-176 / RP-177 # :
| R | G | B | ||||
|---|---|---|---|---|---|---|
| X | = | 0.4123907993 | 0.3575843394 | 0.180487884 | ||
| Y | = | 0.2126390059 | 0.7151686788 | 0.0721923154 | ||
| Z | = | 0.0193308187 | 0.1191947798 | 0.9505321522 |
From one of these matrixes, we can perform the conversion of each R,G,B component to X,Y,Z :
X = (red * 0.4451698156) + (green * 0.2771344092) + (blue * 0.1722826698)
Y = (red * 0.2094916779) + (green * 0.7215952542) + (blue * 0.0689130679)
Z = (red * 0.0000000000) + (green * 0.0470605601) + (blue * 0.9073553944)
We assume the input is linearized :
# Using dark blue :
# Reminder : Red (16 bits) = 0x1212
# Reminder : Green (16 bits) = 0x3434
# Reminder : Blue (16 bits) = 0x5656
red = 0.001016
green = 0.016018
blue = 0.059250
X = (red * 0.4451698156) + (green * 0.2771344092) + (blue * 0.1722826698)
Y = (red * 0.2094916779) + (green * 0.7215952542) + (blue * 0.0689130679)
Z = (red * 0.0000000000) + (green * 0.0470605601) + (blue * 0.9073553944)
>>> print(X, Y, Z)
0.0150991796848652 0.015854455599597 0.0545146231698818
And Voila ! you've made your first XYZ conversion !
Yes, that's possible :)
convert "rgbp3_gamma26.tif" \
-gamma ".38461538461538461538" \ # linearize (1/2.6)
-color-matrix \ # conversion DCI-P3 -> XYZ
"0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.0000000000 0.0470605601 0.9073553944" \
-gamma "2.6" \ # delinearize
"export.tif"
In the first line, we linearize the values (removing gamma 2.6 via its reverse 1/2.6), then we apply the DCI-P3 -> XYZ conversion matrix, finally we delinearize it with a small gamma 2.6.
Keep in mind: this is incomplete, we only apply an XYZ conversion (and a gamma), there are many other steps in the workflow. You will find a complete tool at this address.
If you remember the diagram, there are still a few steps after the XYZ conversion :

To finalize it, we must do :
You can go through the different chapters to expand your understanding. Below, a quick summary for the next steps :
From the last XYZ output, all you need to do is apply a small gamma :
X = pow(X, 1/2.6)
Y = pow(Y, 1/2.6)
Z = pow(Z, 1/2.6)
>>> print(X, Y, Z)
0.19934137226195742 0.20311898286700303 0.326620520884937
And finally, we leave from our [0..1] range to a 16-bit output :
X = (X * 0xFFFF)
Y = (Y * 0xFFFF)
Z = (Z * 0xFFFF)
>>> print(X, Y, Z)
13063.83683118738 13311.402542189044 21405.075836194344
As your can see, there are some decimal numbers in result. This will cause some trouble, because the number 13063.83683118738 gives in hexadecimal 0x464c1f59 which is in 32 bits... we are far from our required 16 or 12 bits :)
The only way is to convert a decimal number (13063.83683118738) to an (unsigned) integer (13063 or 13064).
We will bring them back to an integer with help of type conversion (float → uint16 or uint12) :
X = int(round(X))
Y = int(round(Y))
Z = int(round(Z))
>>> print(X, Y, Z)
13064 13311 21405
>>> print(hex(X), hex(Y), hex(Z))
0x3308 0x33ff 0x539d /* values 16 bits */
These are our values for a X'Y'Z' 10 that we can write in a 16-bit TIF file.
If you want to convert them to 12 bits, we should apply this computation during the "leaving the [0...1] range" step :
X = (X * 0xFFF) /* 4095 */
Y = (Y * 0xFFF) /* 4095 */
Z = (Z * 0xFFF) /* 4095 */
>>> print(X, Y, Z)
816.3029194127156 831.7722348403775 1337.511033023817
X = int(round(X))
Y = int(round(Y))
Z = int(round(Z))
>>> print(hex(X), hex(Y), hex(Z))
0x330 0x340 0x53a /* values 12 bits */
Our values are in 12 bits, we can write them in a 12-bit TIF file.
The official matrix XYZ → DCI-P3 defined in the SMPTE 432-1 - Color Processing for D-Cinema :
| X * | Y * | Z * | ||||
|---|---|---|---|---|---|---|
| R | = | 2.7253940305 | + | -1.0180030062 | + | -0.4401631952 |
| G | = | -0.7951680258 | + | 1.6897320548 | + | 0.0226471906 |
| B | = | 0.0412418914 | + | -0.0876390192 | + | 1.1009293786 |
The official matrix XYZ → sRGB/Rec709 defined in the SMPTE RP-176 :
| X * | Y * | Z * | ||||
|---|---|---|---|---|---|---|
| R | = | 3.2409699419 | + | -1.5373831776 | + | -0.4986107603 |
| G | = | -0.9692436363 | + | 1.8759675015 | + | 0.0415550574 |
| B | = | 0.0556300797 | + | -0.2039769589 | + | 1.0569715142 |
The official matrix XYZ → Rec2020 :
| X * | Y * | Z * | ||||
|---|---|---|---|---|---|---|
| R | = | 1.7166511880 | + | -0.3556707838 | + | -0.2533662814 |
| G | = | -0.6666843518 | + | 1.6164812366 | + | 0.0157685458 |
| B | = | 0.0176398574 | + | -0.0427706133 | + | 0.9421031212 |
From one of these matrixes, we can perform the conversion of each X,Y,Z component to R,G,B :
# Using dark blue :
# Rappel : Red (16 bits) = 0x1212
# Rappel : Green (16 bits) = 0x3434
# Rappel : Blue (16 bits) = 0x5656
# Rappel : red = 0.001016
# Rappel : green = 0.016018
# Rappel : blue = 0.059250
X = 0.0150991796848652
Y = 0.015854455599597
Z = 0.0545146231698818
red = (X * 2.7253940305) + (Y * -1.0180030062) + (Z * -0.4401631952)
green = (X * -0.7951680258) + (Y * 1.6897320548) + (Z * 0.0226471906)
blue = (X * 0.0412418914) + (Y * -0.0876390192) + (Z * 1.1009293786)
print(red, green, blue)
0.0010159999969451862 0.01601799999824417 0.059250000001124806
Due to the imprecision of the XYZ→RGB encoding matrix, we get slightly drifted values compared to the original source, but after converting to 16-bit or 12-bit, you'll get back on track :
# 16-bit Conversion :
>>> print(
hex(int(0.0010159999969451862 * 0xFFFF)),
hex(int(0.01601799999824417 * 0xFFFF)),
hex(int(0.059250000001124806 * 0xFFFF))
)
0x42 0x419 0xf2a
# Compare with references
>>> print(
hex(int(0.001016 * 0xFFFF)),
hex(int(0.016018 * 0xFFFF)),
hex(int(0.059250 * 0xFFFF))
)
0x42 0x419 0xf2a
To observe a drift, you need to go beyond 32 bits per component (with the help of this small tool)
RGB = 0.07058823529411765 0.20392156862745098 0.33725490196078434
XYZ = 0.14604061004705882 0.1851777539607843 0.31560671781803923
RGB = 0.07058823527801708 0.2039215686187231 0.337254901974168
8 bits : 0x12 0x34 0x56
8 bits : 0x12 0x34 0x56
10 bits : 0x48 0xd1 0x159
10 bits : 0x48 0xd1 0x159
12 bits : 0x121 0x343 0x565
12 bits : 0x121 0x343 0x565
16 bits : 0x1212 0x3434 0x5656
16 bits : 0x1212 0x3434 0x5656
20 bits : 0x12121 0x34343 0x56565
20 bits : 0x12121 0x34343 0x56565
24 bits : 0x121212 0x343434 0x565656
24 bits : 0x121212 0x343434 0x565656
28 bits : 0x1212121 0x3434343 0x5656565
28 bits : 0x1212121 0x3434343 0x5656565
30 bits : 0x4848484 0xd0d0d0d 0x15959595
30 bits : 0x4848484 0xd0d0d0d 0x15959595
32 bits : 0x12121212 0x34343434 0x56565656
32 bits : 0x12121212 0x34343434 0x56565656
34 bits : 0x48484848 0xd0d0d0d0 0x159595959
34 bits : 0x48484848 0xd0d0d0d1 0x159595959
# drift on 34 bits
36 bits : 0x121212120 0x343434342 0x565656566
36 bits : 0x121212121 0x343434343 0x565656565
# drift on 36 bits
40 bits : 0x1212121200 0x343434342a 0x5656565665
40 bits : 0x1212121212 0x3434343434 0x5656565656
# drift on 40 bits
48 bits : 0x12121212005e 0x343434342a9b 0x56565656650d
48 bits : 0x121212121212 0x343434343434 0x565656565656
# drift on 48 bits
56 bits : 0x12121212005e2a 0x343434342a9b86 0x56565656650d84
56 bits : 0x12121212121212 0x34343434343434 0x56565656565658
# drift on 56 bits
64 bits : 0x12121212005e2a00 0x343434342a9b8600 0x56565656650d8400
64 bits : 0x1212121212121200 0x3434343434343400 0x5656565656565800
# drift on 64 bits
We observe the drift starting from 34 bits, which gives us a delta since we only go up to 12 bits; And if, in the future, we increase it, we won't reach 32 bits.
After a conversion to RGB (for example), sometimes your values may be out-of-bound, either negative or exceeding the maximum value allowed by the bitdepth.
For example, if your 16-bit value is 65536.370088, you know that you cannot store this value in 16 bits because the maximum value for 16-bit is 65535. You'll need to correct these values.
To do that, no complicated computation, if your values are negative or greater than the maximum value, that means your value is either an absolute white or an absolute black (or « a XYZ color that lies outside the chosen RGB colorspace, commonly referred to as "Out of Gamut" 11). In which case, you only need to overwrite the old value with either 0 or the maxium value allowed by the bitdepth.
For example:
Due to these drifts, don't try - as a last resort or an extreme case - to recover the frame of your movie by converting from your XYZ images. Prefer to keep a DCDM source or one of the original source files in 16 bits or higher.
Even if the drift is minimal, you will lose some information, primarily due to the 12-bit conversion.
Use it only if you have no other choice...
Here are the different reference matrices from the SMPTE :
# RGB DCI-P3 -> XYZ:
0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.2094916779 0.0470605601 0.9073553944
# XYZ -> RGB DCI-P3
2.7254 -1.0180 -0.4402
-0.7952 1.6897 0.0226
0.0412 -0.0876 1.1009
# RGB DCI-P3 -> XYZ
0.4453 0.2770 0.1724
0.2096 0.7216 0.0690
0.0001 0.0470 0.9082
# RGB DCI-P3 -> XYZ - Reference Projector
0.4452 0.2771 0.1723
0.2095 0.7216 0.0689
0.0000 0.0471 0.9074
# RGB DCI-P3 -> XYZ - Reference Projector 10 significant digits
0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.0000000000 0.0470605601 0.9073553944
# XYZ - RGB DCI-P3 - 10 significant digits
2.7253940305 -1.0180030062 -0.4401631952
-0.7951680258 1.6897320548 0.0226471906
0.0412418914 -0.0876390192 1.1009293786
# RGB DCI-P3 -> XYZ
0.4452 0.2771 0.1723
0.2095 0.7216 0.0689
0.0000 0.0471 0.9074
Here are the different matrices collected from the various documents, books or sources. Keep in mind that these matrices may include chromatic corrections in their final values.
# sRGB linear (D65) -> XYZ (Simple, 4 digits) [D65->D65]
X = 0.412453 0.357580 0.180423
Y = 0.212671 0.715160 0.072169
Z = 0.019334 0.119193 0.950227
# sRGB linear (D65) -> XYZ (Better, 5 digits)
X = 0.4124564 0.3575761 0.1804375
Y = 0.2126729 0.7151522 0.0721750
Z = 0.0193339 0.1191920 0.9503041
# SMPTE RP-177 / RP-176 / Glenn Kennel book
X = 0.4123907993 0.3575843394 0.1804807884
Y = 0.2126390059 0.7151686788 0.0721923154
Z = 0.0193308187 0.1191947798 0.9505321522
# XYZ -> RGB Rec709 (SMPTE RP177)
X = 0.4123907993 0.3575843394 0.1804807884
Y = 0.2126390059 0.7151686788 0.0721923154
Z = 0.0193308187 0.1191947798 0.9505321522
# DC28.30 (2006) - Proj Ref.
0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.0000000000 0.0470605601 0.9073553944
# StEM
0.464, 0.2692, 0.1610, 0,
0.2185, 0.7010, 0.0805, 0,
0.0000, 0.0457, 0.9087, 0,
# from Journal SMPTE (October 2009)
| 0.41239080 0.3575843 0.18048079
REC709 -| 0.21263901 0.7151687 0.07219232
| 0.01933082 0.1191948 0.95053215
XYZ = ( 0.950456, 1.000000, 1.089058 )
# from SMPTE RP-431:
# R'G'B' (2.6) -> RGB [] -> XYZ (2.6) -> X'Y'Z'
X = 0.4451698156 0.2771344092 0.1722826698 -> Rdc
Y = 0.2094916779 0.7215952542 0.0689130679 -> Gdc
Z = 0.0000000000 0.0470605601 0.9073553944 -> Bdc
Rdc = 2.7254 -1.0180 -0.4402 -> X
Gdc = -0.7952 1.6897 0.0226 -> Y
Bdc = 0.0412 -0.0876 1.1009 -> Z
# ColorFAQ (https://poynton.ca/notes/colour_and_gamma/ColorFAQ.html)
X ( 0.412453, 0.357580, 0.180423 ) sR
Y ( 0.212671, 0.715160, 0.072169 ) sG
Z ( 0.019334, 0.119193, 0.950227 ) sB
# A Guided Tour of Color Space
# CIE XYZ -> Rec. 709 RGB (D65)
R709 = ( 3.240479, −1.537150, −0.498535 ) * X
G709 = ( −0.969256, 1.875992, 0.041556 ) * Y
B709 = ( 0.055648, −0.204043, 1.057311 ) * Z
------
X = ( 0.412453 0.357580 0.180423 ) * R709
Y = ( 0.212671 0.715160 0.072169 ) * G709
Z = ( 0.019334 0.119193 0.950227 ) * B709
# GammaFAQ (https://poynton.ca/notes/colour_and_gamma/GammaFAQ.html)
Y (luminance) = 0.2126 (R) + 0.7152 (G), 0.0722 (B) = 1.0
# SMPTE RP 177-1993 :
# Luminance Equation :
Y = 0.2126390059 (R) + 0.7151686788 (G) + 0.0721923154 (B) = 1.0
# DCI-HDR-D-Cinema-Addendum
# https://documents.dcimovies.com/HDR-Addendum/54a2b12fba306370323b0ec7de542ade91581047/#sec-C-2
X ( 0.4865709486482242 0.26566769316910 0.19821728523436 ) R
Y ( 0.22897456406975 0.69173852183651 0.07928691409375 ) G
Z ( 0 0.04511338185890 1.04394436890098 ) B
-------------------------------------------------------------------------
R ( 2.49349691194142 -0.93138361791914 -0.40271078445070 ) X
G ( −0.82948896956157 1.76266406031835 0.02362468584193 ) Y
B ( 0.03584583024378 −0.07617238926804 0.95688452400768 ) Z
-------------------------------------------------------------------------
# SMPTE Journal Nov/Dec 2014
# RGB (BT709) to XYZ
X = 0.4124 0.3576 0.1805 * R709
Y = 0.2126 0.7152 0.0722 * G709
Z = 0.0193 0.1192 0.9505 * B709
# XYZ to RGB (BT2020)
R2020 = 0.6370 0.1446 0.1689 * X
G2020 = 0.2627 0.6780 0.0593 * Y
B2020 = 0.0000 0.0281 1.0610 * Z
# Merged R2020->R709
R2020 = 0.6274 0.3293 0.0433 * R709
G2020 = 0.0691 0.9195 0.0114 * G709
B2020 = 0.0164 0.0880 0.8956 * B709
# XYZ->sRGB (FreeDCPPlayer)
sR = { 3.2404542, -1.5371385, -0.4985314 } * X
sG = { -0.9692660, 1.8760108, 0.0415560 } * Y
sB = { 0.0556434, -0.2040259, 1.0572252 } * Z
# XYZ->sRGB (image-engineering.de)
sR = 3.2410 -1.5374 -0.4986 * X
sG = -0.9692 1.8760 0.0416 * Y
sB = 0.0556 -0.2040 1.0570 * Z
# XYZ->sRGB (Franck Chopin)
R = 3.24045416 -0.96926603 0.05564343
G = -1.53713851 1.87601085 -0.20402591
B = -0.49853141 0.04155602 1.05722519
# XYZ->sRGB (RP177, François Helt, Franck Chopin)
R = 3.240575326758 -1.537195988334 -0.498550050270
G = -0.969283339828 1.876044347577 0.041556759645
B = 0.055627459197 -0.203967350390 1.056921724748
# Color and Mastering (Kennel)
X 0.4452 0.2771 0.1723 * R
Y 0.2095 0.7216 0.0689 * G
Z 0.0000 0.0471 0.9074 * B
---------------------------------------------
R 2.7254 -1.0180 -0.4402 * X
G -0.7952 1.6897 -0.0226 * Y
B 0.0412 -0.0876 1.1009 * Z
# SMPTE 432-1-2010 - Digital Source Processing - Color Processing D-Cinema
# Linear RGB -> Linear XYZ
X = 0.4361343357 0.3327206339 0.1888489579 R
Y = 0.2180671678 0.6941240810 0.0878087511 G
Z = 0.0167743975 0.1204678157 0.9262018955 B
# AMPAS Aces
# https://github.com/ampas/aces-dev/blob/v1.0.3/transforms/ctl/README-MATRIX)
# AP0-to-XYZ :
R_out = 0.9525523959 * R_in + 0.0000000000 * G_in + 0.0000936786 * B_in;
G_out = 0.3439664498 * R_in + 0.7281660966 * G_in + -0.0721325464 * B_in;
B_out = 0.0000000000 * R_in + 0.0000000000 * G_in + 1.0088251844 * B_in;
# XYZ-to-AP0 :
R_out = 1.0498110175 * R_in + 0.0000000000 * G_in + -0.0000974845 * B_in;
G_out = -0.4959030231 * R_in + 1.3733130458 * G_in + 0.0982400361 * B_in;
B_out = 0.0000000000 * R_in + 0.0000000000 * G_in + 0.9912520182 * B_in;
# AP1-to-XYZ :
R_out = 0.6624541811 * R_in + 0.1340042065 * G_in + 0.1561876870 * B_in;
G_out = 0.2722287168 * R_in + 0.6740817658 * G_in + 0.0536895174 * B_in;
B_out = -0.0055746495 * R_in + 0.0040607335 * G_in + 1.0103391003 * B_in;
# XYZ-to-AP1 :
R_out = 1.6410233797 * R_in + -0.3248032942 * G_in + -0.2364246952 * B_in;
G_out = -0.6636628587 * R_in + 1.6153315917 * G_in + 0.0167563477 * B_in;
B_out = 0.0117218943 * R_in + -0.0082844420 * G_in + 0.9883948585 * B_in;
# XYZ-to-P3D60 :
R_out = 2.4027414142 * R_in + -0.8974841639 * G_in + -0.3880533700 * B_in;
G_out = -0.8325796487 * R_in + 1.7692317536 * G_in + 0.0237127115 * B_in;
B_out = 0.0388233815 * R_in + -0.0824996856 * G_in + 1.0363685997 * B_in;
# P3D60-to-XYZ :
X_out = 0.5049495342 * R_in + 0.2646814889 * G_in + 0.1830150515 * B_in;
Y_out = 0.2376233102 * R_in + 0.6891706692 * G_in + 0.0732060206 * B_in;
Z_out = 0.0000000000 * R_in + 0.0449459132 * G_in + 0.9638792711 * B_in;
# XYZ-to-P3DCI:
R_out = 2.7253940305 * R_in + -1.0180030062 * G_in + -0.4401631952 * B_in;
G_out = -0.7951680258 * R_in + 1.6897320548 * G_in + 0.0226471906 * B_in;
B_out = 0.0412418914 * R_in + -0.0876390192 * G_in + 1.1009293786 * B_in;
# XYZ-to-REC709:
R_out = 3.2409699419 * R_in + -1.5373831776 * G_in + -0.4986107603 * B_in;
G_out = -0.9692436363 * R_in + 1.8759675015 * G_in + 0.0415550574 * B_in;
B_out = 0.0556300797 * R_in + -0.2039769589 * G_in + 1.0569715142 * B_in;
# XYZ-to-REC2020:
R_out = 1.7166511880 * R_in + -0.3556707838 * G_in + -0.2533662814 * B_in;
G_out = -0.6666843518 * R_in + 1.6164812366 * G_in + 0.0157685458 * B_in;
B_out = 0.0176398574 * R_in + -0.0427706133 * G_in + 0.9421031212 * B_in;
# XYZ -> RGB24
# ref : openjpeg/thirdparty/libtiff/tif_luv.c
R = 2.690*X + -1.276*Y + -0.414*Z
G = -1.022*X + 1.978*Y + 0.044*Z
B = 0.061*X + -0.224*Y + 1.163*Z
Additionally, you'll find a large collection of Input→XYZ or XYZ→Output matrices compiled by Bruce Lindbloom in his article RGB/XYZ Matrices. archive
The unclassifiable (for now) :
(L equals 48 cd/m2)
Have fun with Python and Colour Science :
>>> import numpy as np
>>> import colour
>>> primaries_xyz = [0.64, 0.33, 0.3, 0.6, 0.15, 0.06]
>>> d65_illuminant = colour.CCS_ILLUMINANTS.get('CIE 1931 2 Degree Standard Observer').get('D65')
# array([ 0.3127, 0.329 ])
>>> np.linalg.inv(
colour.normalised_primary_matrix(
primaries_xyz,
d65_illuminant
)
)
array([
[ 3.24096994, -1.53738318, -0.49861076],
[-0.96924364, 1.8759675 , 0.04155506],
[ 0.05563008, -0.20397696, 1.05697151]
])
The result corresponds to the official XYZ → sRGB/Rec709 matrix defined in the SMPTE RP-176.
or you'll find too XYZ/RGB conversions with sRGB_to_XYZ or XYZ_to_sRGB methods
Here are the different files, tools, codes and assets used in this chapter :
Conversion TIFF - from 16-bits to 8-bits : conversion_16bits-to-8bits.py
Conversion TIFF - from 16-bits to 16-bits DCDM (12-bits in 16-bits) : conversion_16bits-to-16bits-DCDM.py
Conversion RGB → XYZ (16-bits) (with Gamma) : conversion_rgb2xyz.py
Conversion XYZ → RGB (16-bits) (with Gamma) : conversion_xyz2rgb.py
Conversion RGB → XYZ (without Gamma) : conversion_rgb2xyz-without-gamma.py
Conversion RGB → XYZ (without conversion in [0..1] range) : conversion_rgb2xyz-without-conv-bitdepth.py
Conversion (complete) RGB-DCI-P3 → X'Y'Z DCI/SMPTE compliant (16 bits) : conversion_dcip3_to_xyz.sh
Conversion (complete) DCI-P3 → X'Y'Z DCI/SMPTE compliant (16 bits) (Python) conversion_dcip3_to_xyz.py
Conversion (complete) DCI-P3 → X'Y'Z DCI/SMPTE compliant (16 bits) (ImageMagick) conversion_dcip3_to_xyz.sh
Conversion (complete) sRGB → X'Y'Z DCI/SMPTE compliant (16 bits) (Python) conversion_srgb_to_xyz.py
Conversion (complete) sRGB → X'Y'Z DCI/SMPTE compliant (16 bits) (ImageMagick) conversion_srgb_to_xyz.sh
Tests out-of-bound : tests_out-of-bound.py
Tests converions drifts : tests_drifts.py
RGB 16-bits : rgb-16bits.tif
XYZ 16-bits : xyz-16bits.tif
XYZ 16-bits (without Gamma) : xyz-16bits-without-gamma.tif
RGB 8-bits : rgb-8bits.tif
XYZ 8-bits : xyz-8bits.tif
RGB 16-bits DCDM (12-bits in 16-bits) : rgb-16bits-DCDM.tif
4K RGB : 4096x2160.rgb.tif
4K XYZ (via ImageMagick) : 4096x2160.xyz.im.tif
4K XYZ (via Python) : 4096x2160.xyz.tif
Reference RGB-DCI-P3 Gamma 3 (2K) : reference_rgbdcip3_gamma26.tif
Reference sRGB (Gamma 2.2) reference_srgb.tif
Reference X'X'Z DCI Compliant (Gamma 2.6) reference_xyz.tif
Output file from conversion_dcip3_to_xyz.py (X'Y'Z' DCI Compliant) : xyz-16bits.tif
SMPTE :
Autres ressources :
Divers ressources :
Some colorspace, such as those developed by ARRI, Sony or Canon have some of their primaries beyond the limits and even have negative values. But there are exceptions (maybe not for long) : 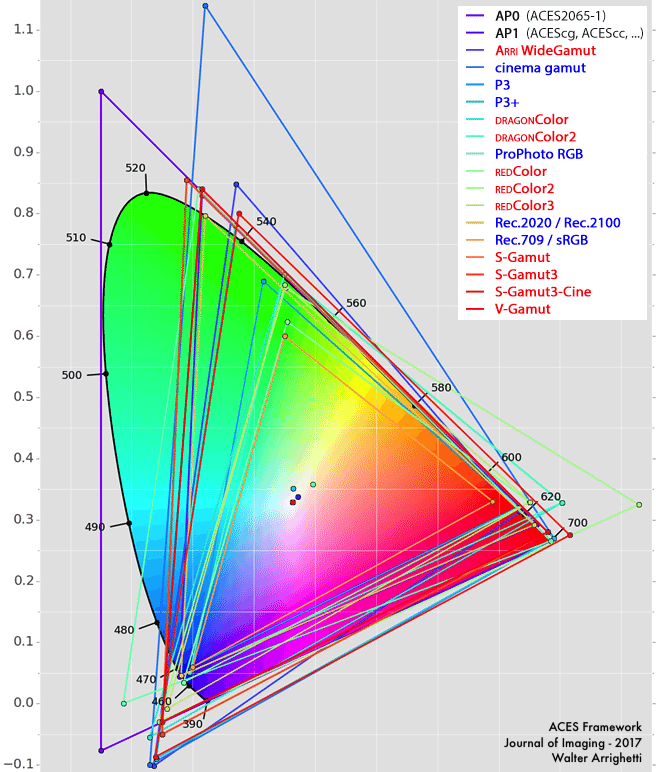 ↩
↩
What X, Y, and Z actually represent : ↩
The XYZ color space is the original model developed by the CIE. The Y channel represents the luminance of a color. The Z channel approximately relates to the amount of blue in an image, but the value of Z in the XYZ color space is not identical to the value of B in the RGB color space. The X channel does not have a clear color analogy. However, if you consider the XYZ color space as a 3-D coordinate system, then X values lie along the axis that is orthogonal to the Y (luminance) axis and the Z axis. -- Understanding Color Spaces and Color Space Conversion
The CIE color model takes the luminance (as measure for perceived brightness) as one of the three color coordinates, calling it Y. The spectral response of the luminance is specified as the photopic luminosity function (..) The coordinate Z responds mostly to shorter-wavelength light, while X responds both to shorter-wavelength and longer-wavelength light. -- Color Spaces (Dr. Rüdiger Paschotta)
CIE XYZ functions are closely related to a linear transform of the LMS cone signals. L = long wavelength, M = middle wavelength, S = short wavelength. -- Fundamentals of Imaging Colour Spaces (Charles A. Wüthrich)
Transformation LMS→XYZ :
[ X ] [ 1.9102 ; -1.1121 ; 0.2019 ][L]
[ Y ] = [ 0.3710 ; 0.6291 ; 0.0000 ][M]
[ Z ] [ 0.0000 ; 0.0000 ; 1.0000 ][S]
Transformation XYZ→LMS :
[ L ] [ 0.3897 ; 0.6890 ; -0.0787 ][X]
[ M ] = [ -0.2298 ; 1.1834 ; 0.0464 ][Y]
[ S ] [ 0.0000 ; 0.0000 ; 1.0000 ][X]
Other matrix : https://psychology.fandom.com/wiki/LMScolorspace
XYZ primaries are hypothetical because they do not correspond to any real light wavelengths. It is additive scheme color spaces, since it define the amounts of three stimuli provided to the eye (the three primaries). (...) XYZ system is based on the color matching experiments. X, Y and Z are extrapolations of RGB created mathematically to avoid negative numbers and are called Tristimulus values. X-value in this model represents approximately the red/green part of a color. Y-value represents approximately the lightness and the Z-value corresponds roughly to the blue/yellow part. -- CIE RGB and CIE XYZ Color Space
The X-value in this model represents approximately the red/green part of a color, the Y-value represents approximately the lightness and the Z-value corresponds roughly to the blue/yellow part. The X value accepts values from 0 to 95.047, the Y-value values from 0 to 100 and the Z-value values between 0 and 108.883. -- XYZ / CIE Color Spaces
In the XYZ color space, Y corresponds to relative luminance; Y also carries color information related to the eye's "M" (yellow-green) cone response. X and Z carry additional information about how the cones in the human eye respond to light waves of varying frequencies. -- Completely Painless Programmer's Guide to XYZ, RGB, ICC, xyY, and TRC
CIE (..) which established color spaces based on colors that can be perceived by the human eye. XYZ does not incorporate negative numbers and instead uses tristimulus values to define the color space that can be seen by the human eye. X represents the linear combination of the cone response non-negative curves created. Y represents luminance and Z is defined as almost equal to blue (blue/yellow) -- How to convert between sRGB and CIE XYZ
Theoretically, the XYZ color space has an infinite volume both in terms of colors and light -- SMPTE Journal, March 2018, Evaluation of Color Pixel Representations for High Dynamic Range Digital Cinema (Boitard, Jacquemin, Damberg, Stojmenovik, Ballestad) ↩
XYZ colorimetry is linear by definition, representing luminance levels that are proportional to the light on the screen. Linear light encoding is convenient for image synthesis and computer graphics because the underlying physics and shading models are linear. However, linear encoding does not match the response of the human visual system, which is approximately logarithmic in nature. -- Color and Mastering for Digital Cinema (Glenn Kennel) ↩
The three components X, Y, and Z of the model represent hue, luminance (light intensity weighted by the eye’s spectral sensitivity), and saturation, respectively. -- Anselme Brice & Gadal Sébastien ↩
Tristimulus: Intensities of the three imaginary colors outside the range of possible chromaticities — X, Y, and Z — used to measure luminance and chromaticity. ↩
Note that this matrix is for the CIE 2-degree, which corresponds to a reference vision with a 2-degree viewing angle (there is also the CIE 10-degree, for peripheral vision): ↩
About the 3x3 matrix : ↩
To be honest, we have 4 matrixes, one for "input sRGB -> output XYZ" and one for "output XYZ -> input sRGB", and the same pair for the RGB DCI-P3 colorspace. ↩
The X'Y'Z' notation show that the XYZ includes its transfer function which is - normally - only the gamma. However, in some documents, the white point normalization is included, and others suggest that the transfer function encompasses the entire equation int( 4095( L * X / 52.37 ) (1/2.6) ), thus combining the white point normalization, the gamma and the bitdepth. ↩
Thanks Rémi ;-) ↩