The transformation to a 12-bit depth (bitdepth or colordepth) is necessary to finalize the process. 1 We are going to see why this choice was made and how to apply this 12-bit conversion.
In this document, I mention bits per component, which means that each component (such as the R in the RGB, or the X in the XYZ) will have a specific size. This size allows more or less informations to be stored for a single component !
For example, "16-bit per component" for the RGB means :
Creating a single color (the merge of the R+G+B) requires 16 + 16 + 16 = 48 bits for a single pixel !
Don't confuse between a 24-bit color and a 24-bit component. A 24-bit component means R24+G24+B24: so, the pixel size is 72 bits. A 24-bit color includes all 3 components, which means you need to divide 24 by the number of components to get the size of one component: 24/3 = 8 bits per component.
There is a large gap in the storage capacity between a 24-bit component and a color encoded in 24 bits.
Throughout all the documentation and the SMPTE standard, we refer only to "bits per component".
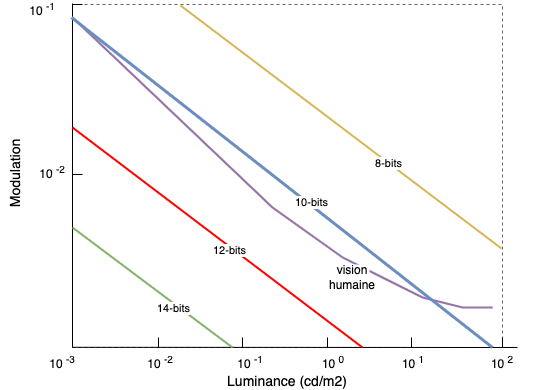
The choice of 12-bit per component is based on the fact that, with 12 bits, the human eye can no longer perceive differences between each steps or potential visual artefacts. We could use more bits by component but that would have required more storage space without providing any practical benefit for projection.
This choice 2 of 12-bit is linked to the Barten model for the contrast sensitivity of human eye. A study shows that below ~11-bit encoding (and others parameters), some artefacts may occur under certain conditions (such as the banding already studied in the chapter Gamma). Beyond this threshold, no artefact is visible.
Based on data from the book Color and Mastering for Digital Cinema, here is an additional graph that allows us to quickly show that human vision has roughly an 11-bit of depth. By choosing a higher bitdepth, we prevent potential issues :
Finally, human vision can distinguish up to 10 millions colors. With 12-bit encoding, we have up to 68 billion colors available 3. That gives some leeway...
The transition from a higher bitdepth to a lower bitdepth requires data conversion, which inevitably leads to data loss.
For example, with a 16-bit depth, we have the ability to encode a color (or component) on 216 = 65.536 values for a single component. In 12-bit, we have 212 = 4096 values available. Thus, we need to reconnect the lost 16-bit values to the available 12-bits values.
In case of reductive conversion (downgrade) from 16-bit to 12-bit, we need to investigate inside the original file because they are some subtilities :
Within the context of a DCDM 4, a TIFF file is considered to have a pseudo 16-bit depth. Each component value is stored in 12 bits but placed in a 16-bit "container" (for example, the component X is encoded in 12-bit and stored using 16 bits). The remaining 4 bits are used for zero-padding. This is a choice established by the SMPTE standard and the DCI specifications to enable a simple conversion between 16 bits and 12 bits. Within this context, we only need to read the first 12 bits and ignore the next 4 bits to obtain our 12 bits by component without losing any data :
Example of a single 12-bit component in a 16-bit container:
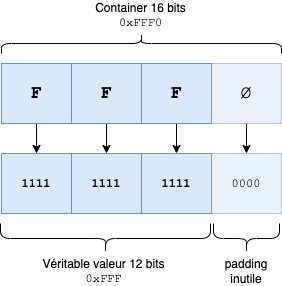
In this case, you will have nothing to do except to retrieve the 12 bits inside the 16 bits
In C, simply use a 4-bits bitshift :
#include <stdio.h>
int main(void) {
int a = 0xFFF0;
printf("%x %d\n", a, a);
printf("%x %d\n", a >> 4, a >> 4);
return 0;
}
# gcc shift.c -o shift && ./shift
fff0 65520
fff 4095
In Python, it's identical :
>>> a = 0xFFF0
>>> a >> 4
4095
>>> hex(a >> 4)
0xfff
In a (true) 16-bit (or higher) per component encoding, a colorimetric conversion is required to map the 16-bit color values to the closest 12-bit color values. For example, in 16-bit, the available values go from 281,474,976,710,656 to 68,719,476,736 in 12-bit, which is 4096 times less of available values. The value used in 16-bit may not exist in 12-bit (in fact, this will be the case most of the time). Thus, a value remapping in the new colorspace is required. For example, we can apply a Lookup Table (LUT): long and time-consuming. Or simply by using the magic of the [0..1] range conversion !
An extreme example of a 16-bit conversion to ... 2-bit depth (223 = 64 available values only) :
In the colorimetric wheel, we have 16 bits per component, which give us 2163 - that is 281,474,976,710,656 available values ... just a 'small' number of combinations. If we downgrade to a 2-bit conversion, we only have 223 = 64 available colors. Above, we performed an image test using only 16 colors, which resulted in the loss of several shades. Thus, we need to remap all the lost colors in the new colorimetric wheel :
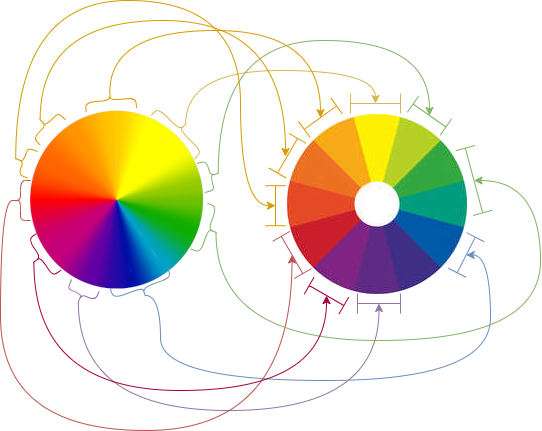
Fortunately, it's possible to convert all 16-bits values to 12-bits values using a simple calculation, which we will see in the following paragraph.
Small reminder and understanding data that we handle, especially the binary and hexadecimal values of certain bitdepths :
| Maximum values | |||
|---|---|---|---|
| Bitdepth | Hexadecimal | Binary | Decimal |
| 8 bits | 0xFF | 1111.1111 | 255 |
| 12 bits | 0xFFF | 1111.1111.1111 | 4095 |
| 16 bits | 0xFFFF | 1111.1111.1111.1111 | 65.535 |
| 16 bits DCDM (\*) | 0xFFF0 | 1111.1111.1111.0000 | 65.520 |
| (\*) 12-bit data in a 16-bit container. The 4 last bits are ignored. | |||
To convert to a different bitdepth, all you need to do is convert the colorimetric values into [0..1] range.
A [0..1] range is defined where the minimum value is 0 (black), the maximum value is 1 (white), and the average value is 0.5 (grey).
From this point, all values are abstract, you can work with them without any limit.
For example, in 16-bit, you divide the maximum value in 16-bit which is 0xFFFF :
# new_value = previous_value / 0xFFFF
>>> 0x0000/0xFFFF # 16-bit black
0.0
>>> 0xFFFF/0xFFFF # 16-bit white
1.0
>>> 0x7FFF/0xFFFF # 16-bit gray
0.49999237048905165 # gray in the [0..1] range
The benefit of this conversion is that you can now convert your 16-bit value to any bitdepth.
To convert your 8-bit gray, all you need to do is multiply by the maximum value of 8-bit depth (255 maximum values, which corresponds to 0xFF)
>>> 0.49999237048905165 * 0xFF
127.49805447470817
127 out of 255 ... We are pretty good with the gray value :)
Using the [0..1] range, you can convert your relative value to any bitdepth.
To finalize the conversion, we convert the float number using a simple type conversion (float → uint16 or uint12) and we apply a simple round() 5 in order to round down to the closest number :
# With the value 127.49
>>> int(127.49805447470817)
127
>>> int(round(127.49805447470817))
127
# With the value 127.51
>>> int(127.51)
127
>>> int(round(127.51))
128
# Finally, convertion to hexadecimal form:
>>> hex(128)
'0x80'
# to check if it really is the average value :
>>> hex(int(round(0xFF / 2)))
'0x80'
The bitdepth is defined to 12 or 16 bits
Here are the different files, tools, codes and assets used in this chapter :
Tools and codes :
Assets :
SMPTE :
Ressources :
The 12-bit conversion can be applied either at the beginning or at the end of the workflow. The advantage of placing it at the end is that you can still work in a larger space during the various conversions, and with greater precision. ↩
Archive: Contrast Sensitivity Experiment to Determine the Bit Depth for Digital Cinema ↩
Limited by its colorspace. Even if you have the possibility of billions of colors, you can be constrained by the colorspace itself. For example, with these different colorspaces overlaid on our visible colors.
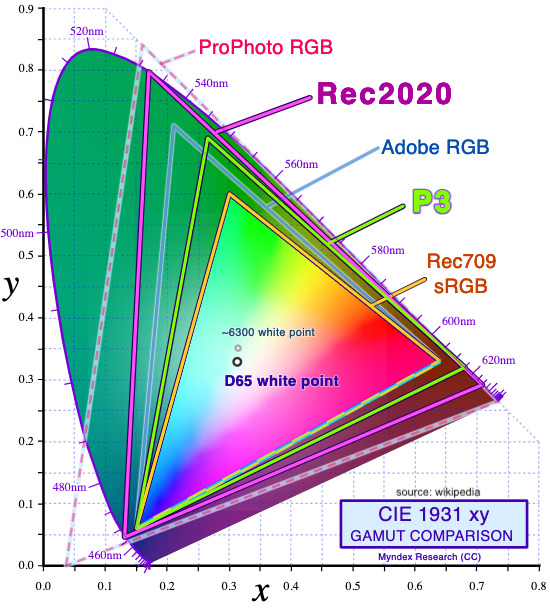The different 'triangles' represent our various color spaces, and the 'horseshoe' shape shows the range of visible colors. You can see that some color spaces are more limited than others, meaning that certain colors won’t be included. So, bitdepth isn’t everything :-) ↩
See SMPTE 428-1 - D-Cinema Distribution Master — Image Characteristics ↩
Rounding is even mandatory : The INT operator returns the value of 0 for fractional parts in the range of 0 to 0.4999... and +1 for fractional parts in the range 0.5 to 0.9999..., i.e. it rounds up fractions above 0.5. -- SMPTE 428-1 - D-Cinema Distribution Master — Image Characteristics ↩
