Un gamma est une "méthode" de transition entre un monde linéaire (informatique par exemple) et un monde non-linéaire (la visualisation). Elle est surnommée "fonction de transfert" par les plus savants et sachants.
Visuellement, un gamma est l'opération qui consiste à jouer avec la luminance. En manipulant le gamma, votre image sera soit plus sombre, soit plus claire. Ce changement de luminance est la résultante de l'intégration d'un gamma et des calculs sous-jacents.
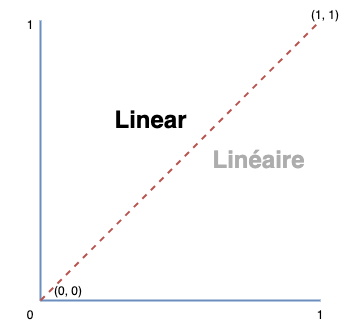
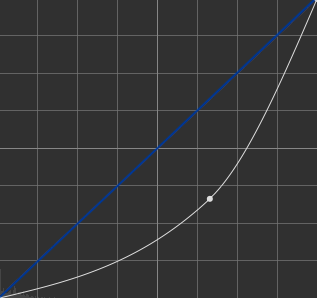
Dans un système linéaire, si nous voulions passer d'un blanc à un noir, il y aura une progression successive et parfaitement rectiligne. Par exemple, si nous disions que notre noir est à 0 et notre blanc est à 1, notre gris parfait serait à 0.5. Cela veut dire que si nous partons de 0 pour monter à 1, nous aurions des paliers intermédiaires parfaitement équilibrés, qui, au final, formerait une ligne parfaitement droite:

Chaque couleur suivante va être équidistant de la couleur d'avant et de la couleur d'après :

Dans notre exemple, avec 10 valeurs entre le noir absolu et le blanc absolu, nous progresserons toujours avec la même valeur (ici, +10, mais vous pourriez avoir n'importe quelle valeur commune)
Une caméra cinéma par exemple va travailler sur du linéaire, chaque photon de lumière va taper un photosite dans le capteur. S'il y a peu de lumière, le capteur traduira moins d'information, s'il a plus de lumière, il traduira plus d'information.
Dans notre monde, l'oeil humain ne travaille pas de la même façon, un oeil va s'adapter à son environnement et essayer de compenser l'obscurité (basse lumière) et la forte luminosité (haute lumière), il est plus sensible aux changements de luminosités qu'aux changements de couleurs, et peut même parfois changer la colorimétrie ambiante en adaptant certaines perceptions des couleurs (par exemple le blanc) par rapport à son environnement 1 : il a une perception non-uniforme de la lumière, il est donc non-linéaire.
Un système non-linéaire va former une courbe plus ou moins déformée. Ici, un exemple avec un gamma utilisant un logarithme :
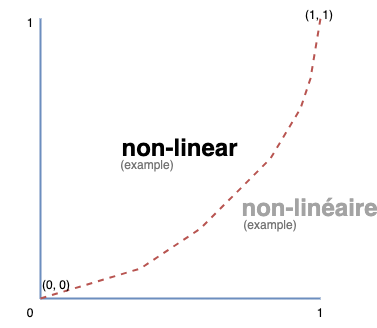
Nous aurons donc une représentation plus de cette forme :

Le passage d'une valeur à une autre va créer une certaine courbe.
Si on doit comparer rapidement avec un exemple linéaire et un exemple non-linéaire :


On remarquera que les blancs sont plus blancs au début, et à la fin, les noirs restent plus dans les noirs.
Un gamma permet à une image de mieux se caler sur notre réelle perception visuelle non-linéaire, on utilisera donc un encodage spécifique à l'image afin d'être le plus proche de cette perception :
| Gamma inférieur à 1.0 | Gamma à 1.0 (neutre) | Gamma supérieur à 1.0 |
|---|---|---|

|

|

|
|
|
|
Un gamma va avoir sa courbe plus ou moins déformée selon sa valeur (2.2, 2.4, 2.6, ...).
On appliquera un gamma selon l'environnement de visualisation : Plus la pièce est sombre, plus le nombre du gamma sera haut, plus la pièce aura de la luminosité, plus le nombre du gamma sera bas :
Alors, pourquoi on utilise un gamma 2.6 ? Pourquoi pas un 2.8 ? ou un 3.0 ?
Déjà parce que la salle se trouve être dans une condition spécifique par rapport aux autres environnements (au bureau, vous aurez plus de lumière, dans votre salon peut-être un peu moins, etc...), la salle est dans une obscurité quasi totale, nous pouvons donc accentuer le contraste de l'image.
L'autre aspect est qu'un gamma 2.6 est le plus proche de la vision humaine dans ce contexte de quasi obscurité. 3 :
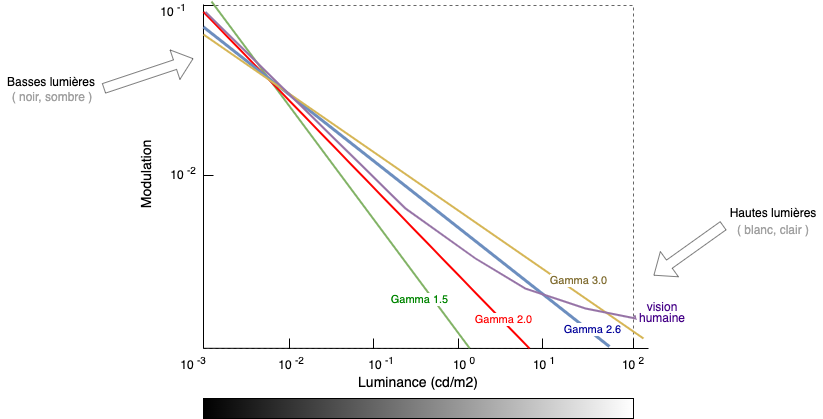
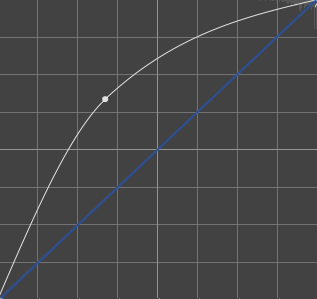
Basé sur les données du livre Color and Mastering for Digital Cinema, le graphe montre clairement que le gamma 2.6 est celui qui se rapproche le plus de la vision humaine.
Dans la partie en haut à gauche, se trouvent les basses lumières (noir, sombre) et dans la partie en bas à droite, les hautes lumières (blanc, clair). Il faut arriver à jouer entre les différents paliers des différentes valeurs afin de rester toujours en dessous du seuil de détection de la vision humaine et aussi ne pas trop gaspiller en valeurs.
La courbe violette correspondant à la vision humaine; il faut qu'elle soit autant que possible en dessous pour avoir une image sans banding. Le color banding est un passage d'une couleur à une autre trop brutalement. Ces bandes de couleurs peuvent apparaître également selon le choix du bitdepth ou le choix de l'espace colorimétrique (gamut) utilisé, ce n'est pas forcément qu'à cause d'un mauvais gamma. Vous pouvez remarquer ces bandings - le plus souvent - par exemple sur un flux TV ou via un DVD, et notamment sur les zones sombres. Voici quelques exemples de color banding sur des images de trailers :
Il est important de comprendre que l'application d'un gamma est avant tout un choix technique: un gamma permettra d'avoir des gradients (passage d'une valeur à une autre) moins visibles à l'oeil humain. Les changements de valeurs trop brutaux sont plus perceptibles. Une courbe gamma permet d'avoir des valeurs en dessous du seuil de la vision humaine (en violet).
De toutes les valeurs de gamma possibles, le gamma 2.6 est au final un bon compromis.
Modifier un gamma, c'est linéariser ou délinéariser, les deux nécessitent un type de calcul utilisant le principe de la loi de puissance (power law) sur un gamma à 2.6 (à adapter suivant l'input) en input et 1/2.6 en output (DCI).
N'oubliez pas que l'utilisation du symbole prime ' désigne un gamma. Ainsi, un X'Y'Z' est un XYZ avec un gamma intégré. 4
Voici quelques exemples sur la transformation gamma entre un R'G'B' et un X'Y'Z' et inversement :

De notre R'G'B', on enlève sa courbe gamma 2.6 (mais qui sera très probablement plutôt un 2.2), ça nous donne un RGB linéaire (1.0); A partir de là, nous convertissons en XYZ, puis on applique un petit gamma 2.6 (1/2.6) pour donner un XYZ avec gamma : X'Y'Z'.
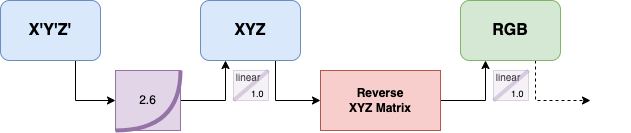
Ici, c'est l'inverse, nous avons un XYZ avec gamma (X'Y'Z'), on enlève son gamma 2.6 (en bleu), ce qui nous donne un XYZ linéaire (sans gamma, ou plutôt un gamma 1.0) et après conversion inverse, nous arrivons sur notre RGB. De là, nous pouvons aller sur d'autres types de conversions.
Dans les exemples, nous travaillerons sur du 16 bits pour être plus précis.
Dans notre documentation, pour appliquer la loi de puissance dans nos calculs, nous utiliserons la fonction pow().
En mathématique, notre pow() est une simple équation : f(x) = a.xg.
La variable g étant notre valeur de gamma, soit 2.6, soit 1/2.6.
En Python - et dans d'autres langages - vous pouvez utiliser la fonction pow() ou la double-étoile :
>>> pow(1.5, 2.6)
2.8697051264080295
>>> (1.5**2.6)
2.8697051264080295
En C et C++, vous utiliserez la fonction powf() :
#include <stdio.h>
#include <math.h>
int main(void) {
float a = 1.5;
float g = 2.6;
printf("%.022f\n", powf(a, g));
return 0;
}
# gcc powfy.c -o powfy && ./powfy
2.8697049617767333984375
Dans le reste de notre documentation, nous utiliserons la fonction pow() pour s'accorder sur plusieurs langages de programmation.
"Supprimer" un gamma, c'est revenir à un gamma 1.0 :
| Gamma 0.38 (`1 / 2.6`) | Gamma 2.6 | Gamma à 1.0 (neutre) | ||
|---|---|---|---|---|

|
+ |

|
= |

|
Pour rendre un gamma neutre, il suffit :
2.6 sur un gamma 1/2.6. 1/2.6 sur un gamma 2.6. A partir de là, nous pouvons voir les différents calculs dans les paragraphes suivants.
C'est un petit dilemme. Par défaut, il n'y a pas de métadonnées indiquant le gamma (sauf si le fichier permet d'inclure ce type de métadonnées), il faut donc le connaître par rapport à son espace colorimétrique :
| Niveau | Utilisation |
|---|---|
| 2.2 | sRGB, ... |
| 2.35 | Rec709 EBU Standard (rarement utilisé) |
| 2.4 | Rec709 pour compenser des contrastes elevés sur certains moniteurs, Rec2020 |
| 2.6 | DCI P3 |
Notez que même s'il existe une normalisation (ou un standard) pour tel type d'espace colorimétrique et qui va définir un gamma spécifique (par exemple, le gamma d'un sRGB est normalisé à 2.2), vous pouvez tomber sur un RGB avec un gamma 2.6 ou même 2.0 : le créateur d'une image peut vouloir définir un gamma plus ou moins prononcé pour différentes raisons (même les plus folles :)
Vérifiez donc bien le gamma d'entrée est le bon gamma défini dans sa normalisation.
Petit résumé des gammas DCI d'entrée et de sortie avant de poursuivre :
1/2.61/2.6 en appliquant un gamma 2.62.6Appliquer un gamma 2.6 peut être effectué dans deux cas :
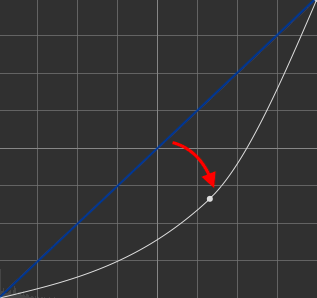
Si vous êtes sur un gamma 1.0 (neutre), |
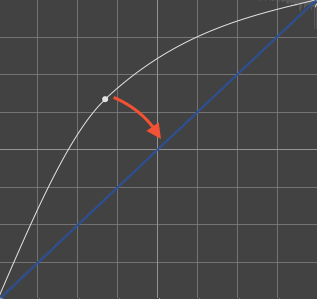
Si vous êtes sur un gamma 1 / 2.6, |
Pour mieux comprendre la conversion gamma, voici un premier exemple sans la conversion plage [0...1] et utilisation de la fonction pow() que nous trouverons dans d'autres langages de programmation :
$ python3
r = pow(0xFFFF, 2.6) # 0xFFFF = valeur décimale "65535"
3332963746773.969
g = pow(0xFFFF, 2.6)
3332963746773.969
b = pow(0xFFFF, 2.6)
3332963746773.969
Dans la couleur blanche, le rouge, le vert et le bleu seront au maximum, donc à 0xFFFF.
Pour notre exemple, j'utilise la valeur hexadécimale 0xFFFF parce que j'ai l'habitude de travailler directement avec les valeurs visibles en analysant un fichier (en hexadécimal), mais il est préférable de travailler avec des valeurs décimales, donc 65535 dans notre cas.
Remarquez que nous travaillons avec des valeurs (hexadécimales ou décimales) brutes : utiliser des valeurs de la sorte est source de problème : Les valeurs flottantes en sortie de pow() sont d'une grande taille, excessive et inutile, dans un workflow mathématique et pouvant apporter des problèmes dans les précisions. Pour cela, il est préférable de normaliser tout ceci est de travailler sur une base plus saine : dans une plage [0..1]. Pour rappel, mettre une valeur dans une plage [0..1], c'est simplement convertir n'importe quelle valeur décimale brute vers une valeur entre 0.0 et 1.0.
Maintenant, voyons un exemple avec la conversion plage [0..1].
Pour cela, vous divisez votre valeur colorimétrique par sa valeur maximale dans le bitdepth (ici 16 bits, donc 0xFFFF) :
$ python3
VALEUR_MAX_16BITS = 0xFFFF # 65535
r = pow(0xFFFF / VALEUR_MAX_16BITS, 2.6)
1.0
g = pow(0xFFFF / VALEUR_MAX_16BITS, 2.6)
1.0
b = pow(0xFFFF / VALEUR_MAX_16BITS, 2.6)
1.0
Avec la plage [0..1], c'est plus parlant : nos valeurs minimales et maximales en sortie de pow() seront toujours soit 0.0 (min) ou soit 1.0 (max).
Notez qu'avec un bitdepth à 12 bits, nous aurions quasiment le même résultat :
# Conversion gamma en 16 bits
>>> pow(0x7FFF / 0xFFFF, 2.6) # 0x7FFF = 32767 / 0xFFFF = 65535
0.16493194524645807
# Conversion gamma en 12 bits
>>> pow(0x7FF / 0xFFF, 2.6)
0.16483378645422764
La différence entre 16 et 12 bits est normal, la précision n'étant pas la même, la loi de puissance (pow) sera légèrement différente à la fin, cependant on constate que nous avons deux 0.164
Notre premier exemple sans passer par la conversion plage [0..1] :
r = pow(0x1212, 2.6) # valeur décimale: 4626 (sur 65535)
3384812638.485899
g = pow(0x3434, 2.6) # valeur décimale: 13364 (sur 65535)
53386913590.93187
b = pow(0x5656, 2.6) # valeur décimale: 22102 (sur 65535)
197479534076.03644
Et avec la conversion plage [0..1] :
VALEUR_MAX_16BITS = 0xFFFF # 65535
r = pow(0x1212 / VALEUR_MAX_16BITS, 2.6)
0.0010155563923436356
g = pow(0x3434 / VALEUR_MAX_16BITS, 2.6)
0.016017850071908507
b = pow(0x5656 / VALEUR_MAX_16BITS, 2.6)
0.05925042967154389
Avec ces valeurs, vous êtes linéarisés.
1/2.6Appliquer un gamma 1/2.6 peut être effectué dans deux cas :
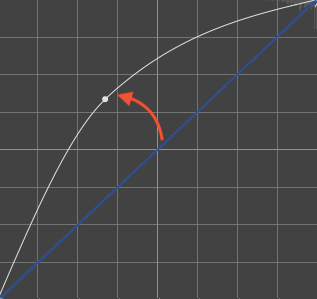
Si vous êtes sur un gamma 1.0 (neutre), |
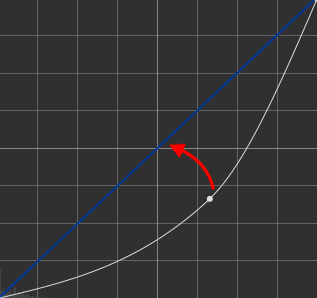
Si vous êtes sur un gamma 2.6, |
1/2.6 :Nous allons reprendre les valeurs linéarisés du blanc :
Sans passer par la conversion plage [0..1] :
r = pow(3332963746773.969, 1/2.6)
65534.99999999996
>>> hex(int(round(65534.99999999996)))
'0xffff'
g = pow(3332963746773.969, 1/2.6)
65534.99999999996
b = pow(3332963746773.969, 1/2.6)
65534.99999999996
Avec la couleur blanche, on remarque que notre valeur de sortie est (quasiment) à la valeur maximale en 16 bits (65535). Si nous appliquons un petit round() et hex(), notre valeur de la couleur blanche est bien 0xFFFF.
Ou en passant par la conversion plage [0..1] sur la couleur bleu foncé :
>> VALEUR_MAX_16BITS = 0xFFFF # 65535
# (R)
>> pow(0.0010155563923436356, 1/2.6) * VALEUR_MAX_16BITS
4626.000000000001
>>> hex(4626)
'0x1212'
# (G)
>> pow(0.016017850071908507, 1/2.6) * VALEUR_MAX_16BITS
13364.000000000002
>>> hex(13364)
'0x3434'
# (B)
>> pow(0.05925042967154389, 1/2.6) * VALEUR_MAX_16BITS
22102.0
>> hex(22102)
'0x5656'
Nos valeurs sont 0x1212, 0x3434 et 0x5656, comme auparavant.
Voici les différents fichiers, outils, codes et assets utilisés dans ce chapitre :
Outils et codes :
Conversion TIFF 16-bits à 8-bits : conversion_16bits-to-8bits.py
Conversion TIFF 16-bits à 16-bits DCDM (12-bits dans du 16-bits) : conversion_16bits-to-16bits-DCDM.py
Conversion RGB → XYZ (16-bits) (avec Gamma) : conversion_rgb2xyz.py
Conversion XYZ → RGB (16-bits) (avec Gamma) : conversion_xyz2rgb.py
Conversion RGB → XYZ (sans Gamma) : conversion_rgb2xyz-without-gamma.py
Conversion RGB → XYZ (sans conversion plage [0..1]) : conversion_rgb2xyz-without-conv-bitdepth.py
Tests out-of-bound : tests_out-of-bound.py
Tests Dérivations de conversions : tests_drifts.py
Assets :
RGB 16-bits : rgb-16bits.tif
XYZ 16-bits : xyz-16bits.tif
XYZ 16-bits (sans Gamma) : xyz-16bits-without-gamma.tif
RGB 8-bits : rgb-8bits.tif
XYZ 8-bits : xyz-8bits.tif
RGB 16-bits DCDM (12-bits dans du 16-bits) : rgb-16bits-DCDM.tif
Ressources :
Autres ressources :
C'est notamment pour cela que si vous êtes à l'extérieur d'une maison et que vous regardez une pièce, vous verrez par exemple des couleurs chaudes (jaune, orange) et si vous venez à l'intérieur, après un petit moment, vous ne ressentirez plus (ou moins) ces couleurs chaudes. L'oeil se sera adapté. Pour en savoir plus, lire par exemple la page "Adaptation visuelle" (https://fr.wikipedia.org/wiki/Adaptation_visuelle) ↩
Références à l'application d'un gamma 2.6 dans le processus de transformation : ↩
Color conversion from R’G’B’ to X’Y’Z’ requires a three-step process which involves linearizing the color-corrected R’G’B’ signals (by applying a 2.6 gamma function) -- SMPTE RP-431-2-2011 - DCinema Quality Reference Projector and Environement - Chapitre « Color Conversion to XYZ »
The digital files were linearized (applying a gamma of 2.6), then a 3x3 matrix was applied to convert RGB to XYZ, followed by application of the 1 / 2.6 gamma function. The finished color-corrected files were stored as 12-bit X'Y'Z' data in 16-bit TIFF files. -- Color and Mastering for Digital Cinema (Glenn Kennel)
First, the R’G’B’ data is linearized by applying a simple gamma 2.6 transfer function : R = ( R / 4095 ) 2.6 -- SMPTE RP-431-2-2011 - DCinema Quality Reference Projector and Environment - Chapitre « Color Conversion to XYZ »
Et aussi minimiser le nombre de bits nécessaires à l'encodage, éviter l'effet coutourning dans le rendu de l'image et avoir une meilleure répartition des différents niveaux de valeurs dans un encodage qui peut être restreint (ici en 12 bits). ↩
La notation X'Y'Z' indique que le XYZ est accompagné de sa fonction de transfert qui est -normalement- que le Gamma. Cependant, dans certaines documentations, ils intègrent aussi la normalisation du point blanc et d'autres encore laissent supposer que la fonction de transfert englobe toute l'équation int( 4095( L * X / 52.37 ) (1/2.6) ), donc la normalisation du point blanc, le gamma et le bitdepth. ↩