JPEG2000 : Le format d'image utilisé dans le cinéma numérique


CE CHAPITRE SE VEUT ÊTRE ACCESSIBLE À TOUS

Le format JPEG2000 possède un large spectre de fonctionnalités. La version utilisée dans le cinéma est limitée à certaines d'entre elles. Je n'évoquerais donc pas l'ensemble des possibilités du JPEG2000 (ce qui serait trop vaste et en dehors de notre scope) mais seulement le JPEG2000 dans un contexte cinéma numérique (DCP & IMF)

Pour les ondelettes (wavelet) - utilisées dans le JPEG2000 - nécessitent des compétences en mathématique. Certains passages seront donc très (trop) simplifiés afin de permettre à tous de comprendre les bases et ne laisser personne sur le bord de la route. Le but n'étant pas de finir le chapitre en créant notre propre encodeur JPEG2000 (quoique ? ;-) mais au moins que - lorsque nous manipulerons du JPEG2000, par exemple via des librairies, des programmes ou des encodeurs physiques, nous puissions comprendre le moindre des paramètres internes et leurs implications dans le rendu final.

Les ondelettes ont des concepts mathématiques très complexes. Pour le bien de tous, nos exemples seront donc très simplifiés. Gardez en tête que ce qui a été simplifié dans ce paragraphe sont des équations et des algorithmes très complexes derrière. Certains en font même des thèses... :-)

Le but étant d'être détendu avec certaines notions observées dans les normes SMPTE et spécifications DCI sur le JPEG2000 et également lors de manipulation du JPEG2000.

Préface

Le JPEG2000 a été sélectionné parmi un panel de plusieurs autres méthodes de compressions et décompressions.

Le JPEG2000 a un avantage avec sa compression basée sur les ondelettes - la transformation en Ondelettes Discrète (Discrete Wavelet Transform ou DWT) - ce qui permet lors d'une compression plus ou moins accentuée, une image nette (compression basse) ou un peu plus floue (compression forte) au lieu d'artefacts de compression classique qui se manifestent par des blocs de pixelisation 1.

L'autre avantage est que dans un 4K, vous aurez aussi une version 2K 2 . Cela veut donc dire que pour générer du 4K, vous générer en même temps le 2K en une seule passe d'encodage !

Le JPEG2000 supporte à la fois la compression avec perte, destructive (utilisée pour le DCP) et sans perte, donc non destructive (utilisée pour l'IMF / DCDM).

Le JPEG2000 permet d'avoir des qualités différentes dans différentes zones de l'image. Très utile au cinéma où la zone d'intérêt est surtout au centre de l'image 3 . Vous pourriez avoir une compression forte sur l'ensemble de l'image sauf sur les visages des acteurs ou actrices par exemple.

La base du JPEG2000 (Core Coding System) est orientée royalty-free.

Pour comprendre la méthode de compression multi-résolutions du JPEG2000, il faut faire une petite incursion dans le monde magique des ondelettes (wavelets)

Les transformations par ondelettes (wavelet transform)

Déjà, il faut savoir qu'il existe plusieurs types d'ondelettes (Haar, Db, Fwt, ...). Appelées familles, vous pourrez avoir plusieurs ondelettes dans un type spécifique.

Le JPEG2000 utilise une famille particulière, celle des transformées en ondelettes discrètes (Discret Wavelet Transform ou surnommé DWT) intégrant notamment la décomposition multirésolution.

Historiquement, la première "ondelette" a été créée par Alfred Haar fr en 1909.

En comprenant son principe, on comprend les autres types d'ondelettes qui sont venues par la suite et utilisent des mécanismes et des équations encore plus complexes dont notamment celles utilisées par le JPEG2000.

Les deux types ondelettes utilisés dans le JPEG2000 sont celles de Ingrid Daubechies fr et celles de Didier Le Gall & Ali J. Tamatabai, et surnommées :

Celle que nous utiliserons dans le DCP est donc l'ondelette Daubechies 9/7.

Avant d'attaquer les ondelettes Daubechies, qui sont relativement complexes au premier abord, nous allons d'abord étudier les bases des ondelettes.

Les bases des ondelettes

Pour comprendre le principe des ondelettes, nous allons utiliser et étudier une version simplifiée.

Normalement, les ondelettes intègrent 4 composantes essentielles :

Pour nos besoins en simplification, nous allons tout d'abord écarter ces concepts et clarifier tout ceci avec un gros travail de vulgarisation. Les plus matheux voudront bien m'excuser, l'objectif étant de comprendre la "big picture" du principe des ondelettes, le sujet étant très vaste et très mathématique, il est préférable de simplifier à outrance.

Dans la suite du paragraphe, je vais éviter au possible de balancer des équations, juste pour balancer de l'équation qui ne nous serviront aucunement à comprendre sans avoir un certain niveau de mathématique. Le but ultime étant de comprendre comment fonctionne le JPEG2000 dans notre cas.

Avant de partir sur notre route des calculs, partons d'une simple image en noir et blanc (plus simple car on ne s'occupera que d'une composante de couleur) :

Prenons chaque valeur de chaque pixel sur différents niveaux noir, blanc et gris pour les poser sur un graphe idéal: le premier pixel de notre image sera au tout début de notre graphe et le dernier pixel en toute fin :

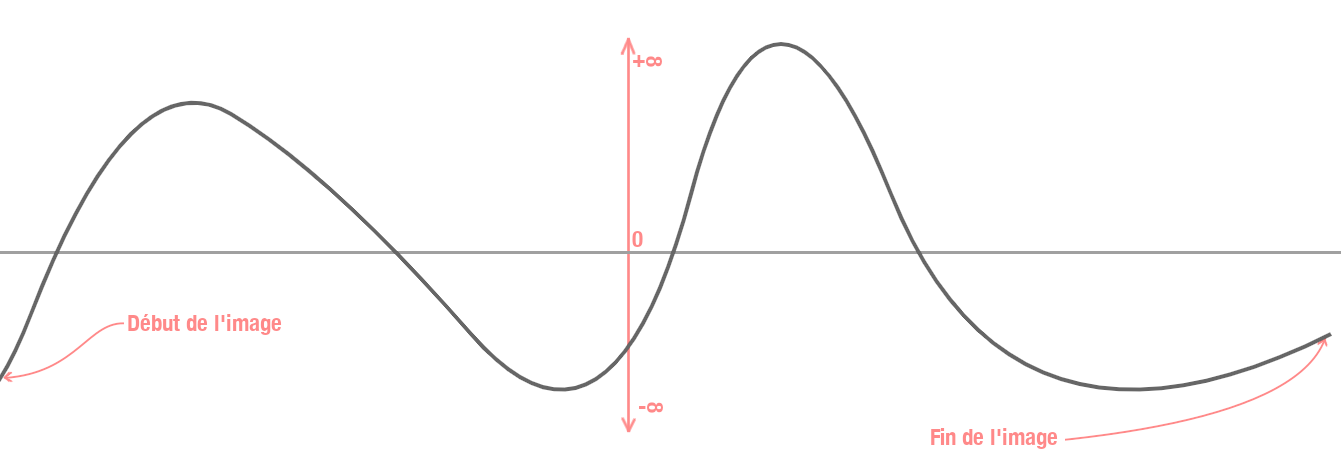
Pour interpréter cette courbe, imaginez juste que les points les plus bas sont les plus sombres et les points les plus hauts, les plus lumineux. Cette courbe est idéale et surtout imaginaire. En vérité, notre graphe ressemblerait plutôt à cela, où chaque point d'escalier représente véritablement les valeurs de nos pixels :

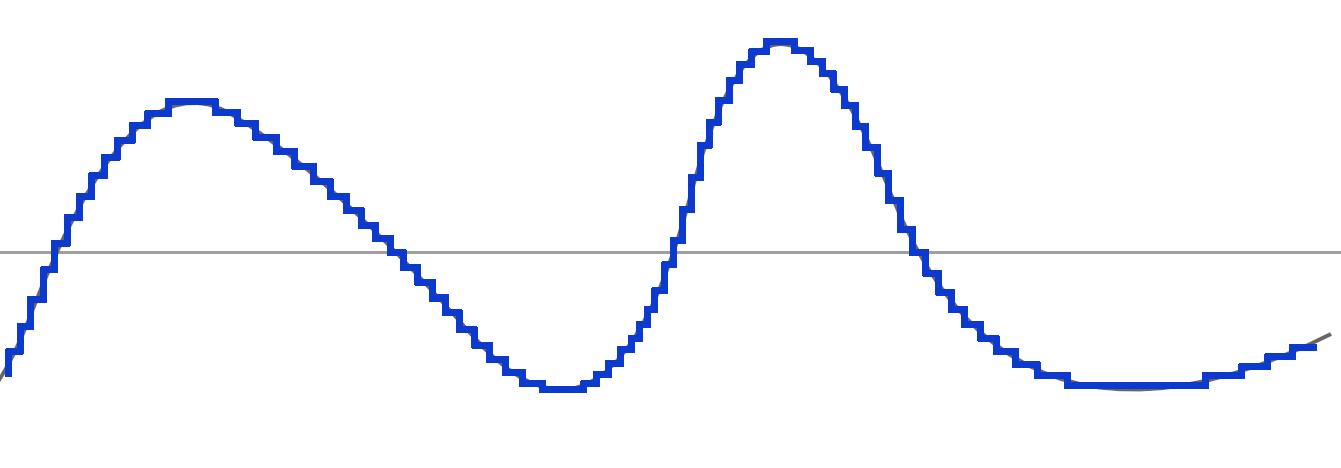
Chaque point représente la valeur d'un pixel selon un certain bitdepth (8, 16, 24, etc..). Les escaliers sont un peu énormes pour notre exemple (nous pourrions avoir une plus grande finesse dans les valeurs avec un bitdepth plus haut).

Nous ne sommes pas encore dans la partie ondelette, nous posons juste la base de ce qu'est une image numérique : une série de valeurs avec un minimum (0) et un maximum (255 par exemple).

Le principe primaire des ondelettes est d'avoir deux fonctions : une fonction de scaling et une fonction wavelet qui vont toutes les deux travailler ensemble pour décomposer ou recomposer l'image.

Pour comprendre l'utilité, nous allons procéder à la première étape, celle de calculer la "moyenne entre deux points".

Si vous regardez bien le graphe suivant, vous verrez que notre courbe verte va traverser notre courbe bleue à certains endroits en son milieu, c'est parce que nous avons effectué une moyenne entre les deux points :

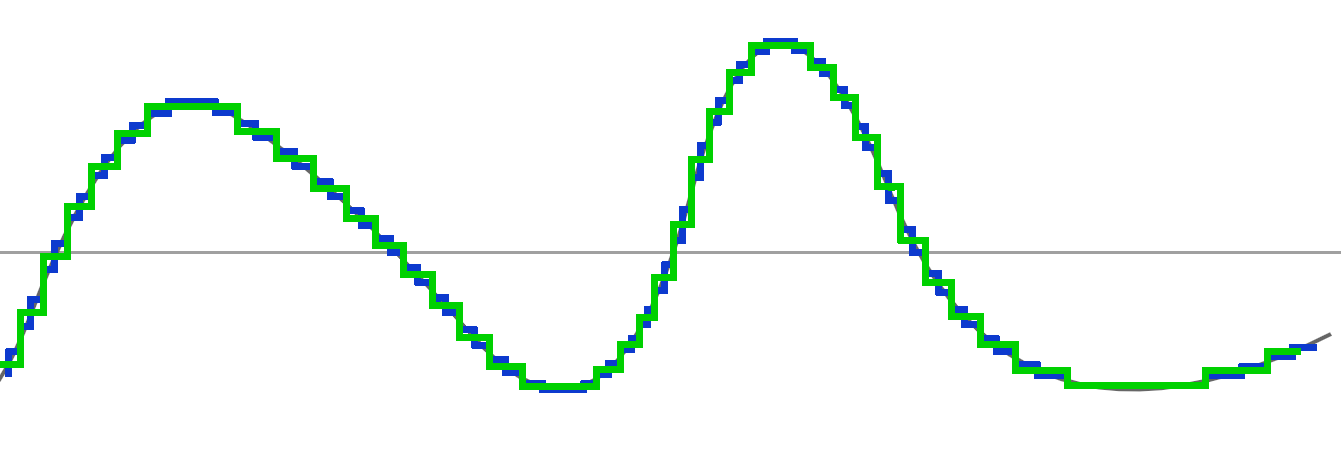
Si nous enlevons notre approximation précédente et nous gardons notre nouvelle "moyenne", voila le résultat :

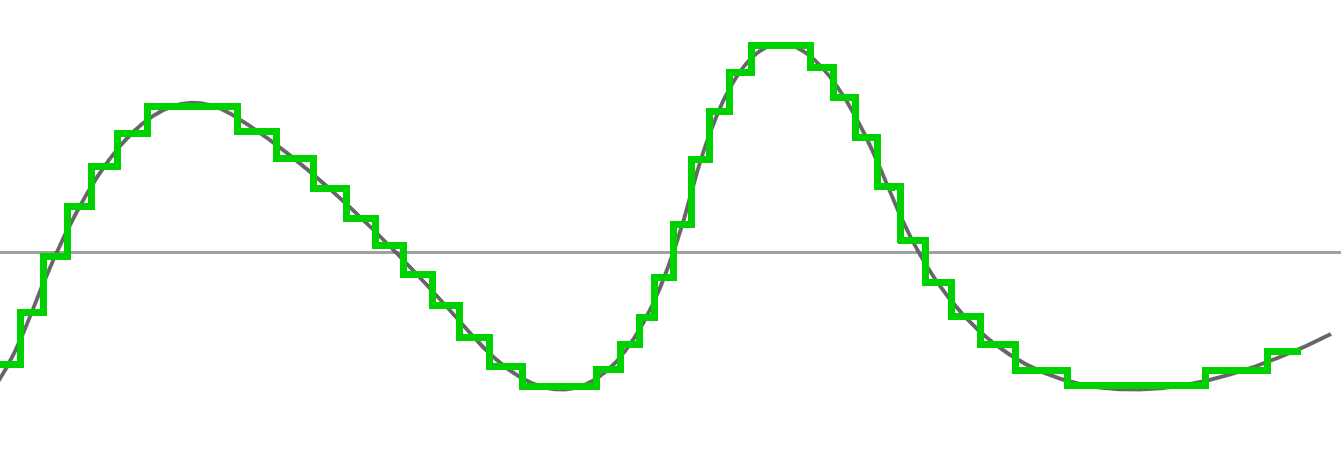
Nous restons assez proches de la première courbe, cependant, vous remarquez que nous avons moins de points, donc moins de données.

Avec cette nouvelle approximation, nous effectuons une nouvelle passe "moyenne" :

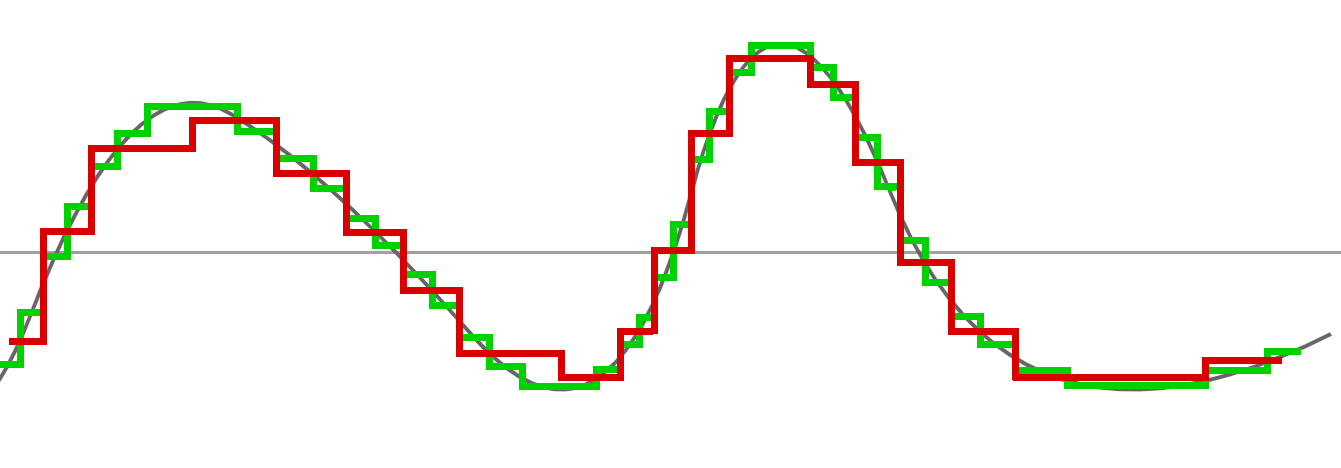
Notre nouvelle ligne rouge reste encore assez proche de notre première courbe :

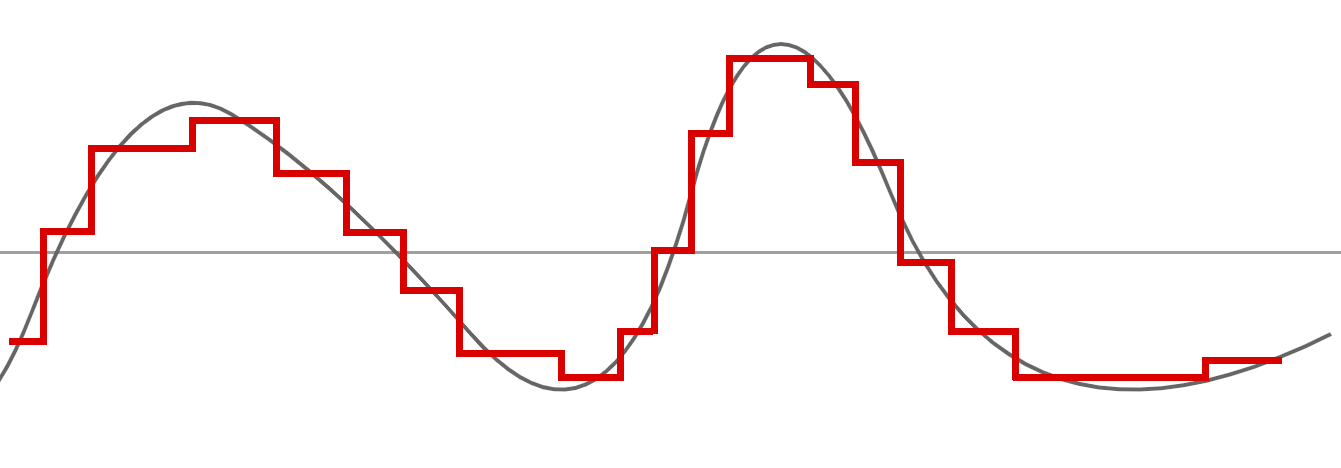
Et nous effectuons -encore- une nouvelle passe de moyenne sur l'approximation rouge :

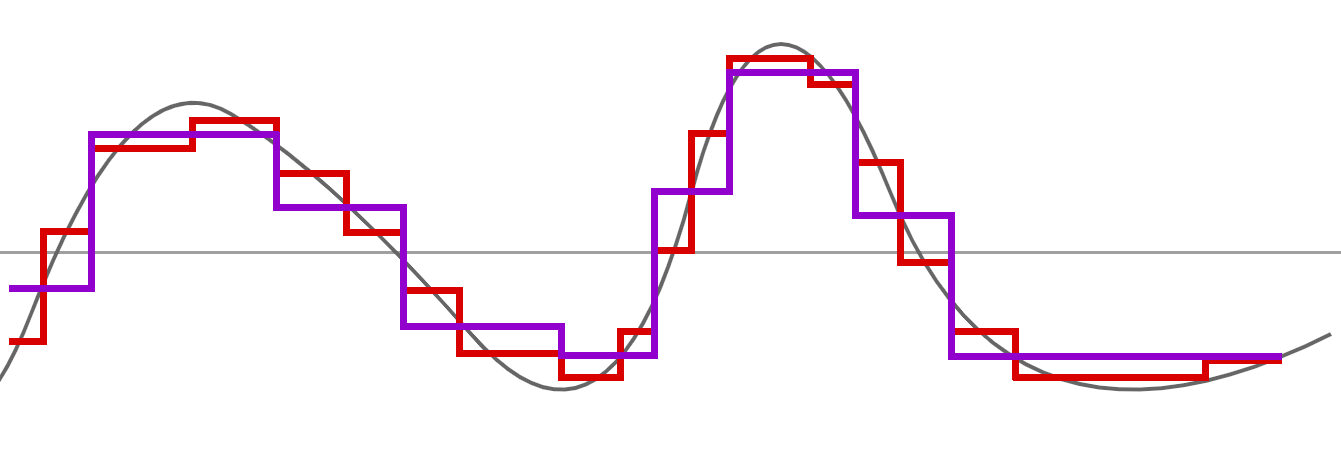
Ce qui nous donne une très grosse approximation :

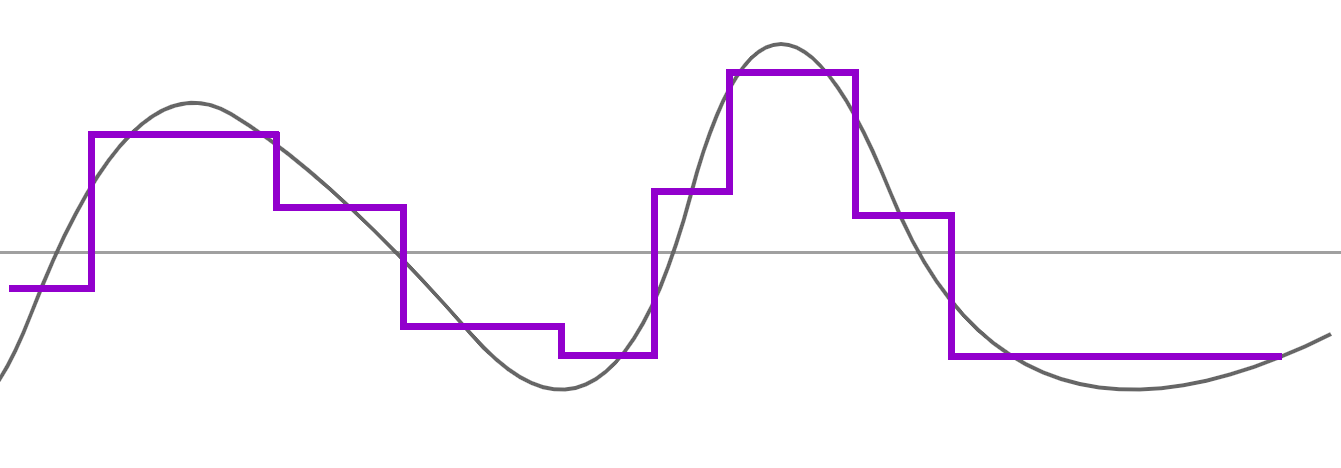
Nous pourrions continuer mais cela n'aurait aucun intérêt car nous allons arriver à un niveau où nous n'aurons plus assez de données pour représenter quelque chose (à la fin, nous n'aurions plus qu'une ligne droite...)

Chaque "passe" de moyenne représente une résolution différente. Ainsi la toute première peut représenter notre image en 2K et la toute dernière, notre image en 128x68.

Si on combine les différentes passes, nous voyons l'évolution des différentes décompositions à travers ces moyennes appliquées :

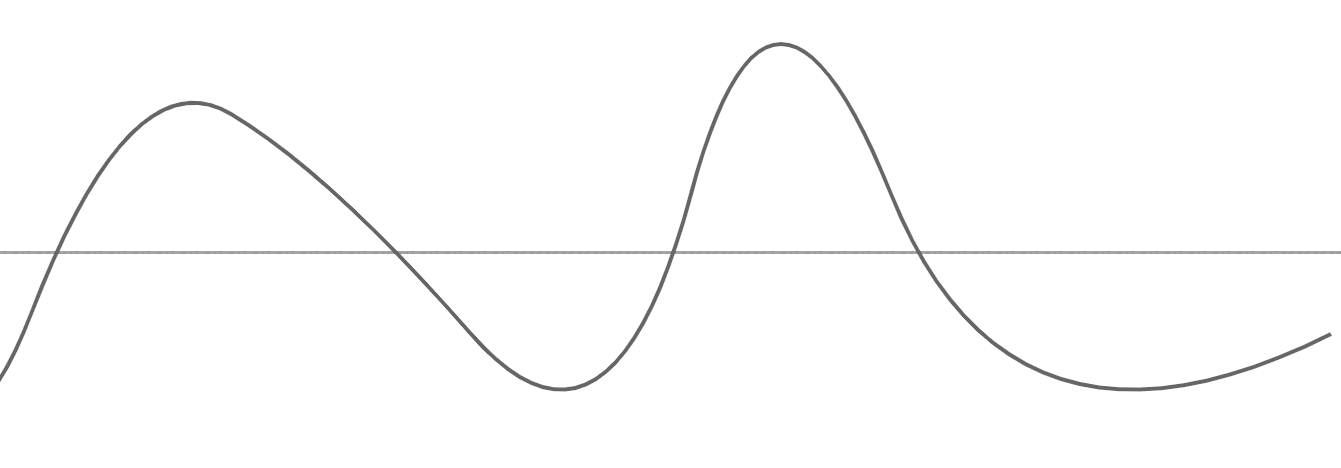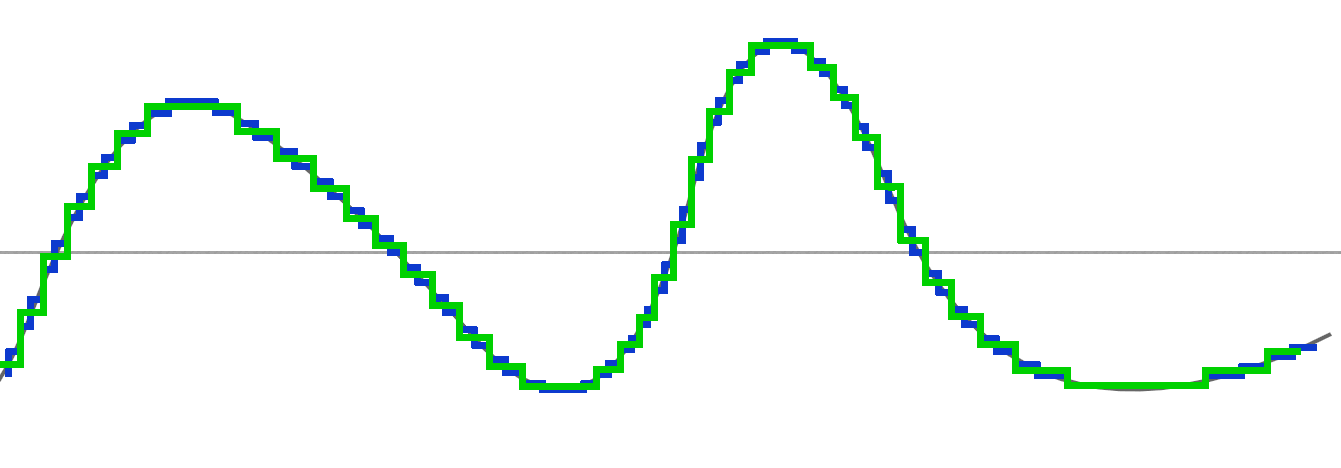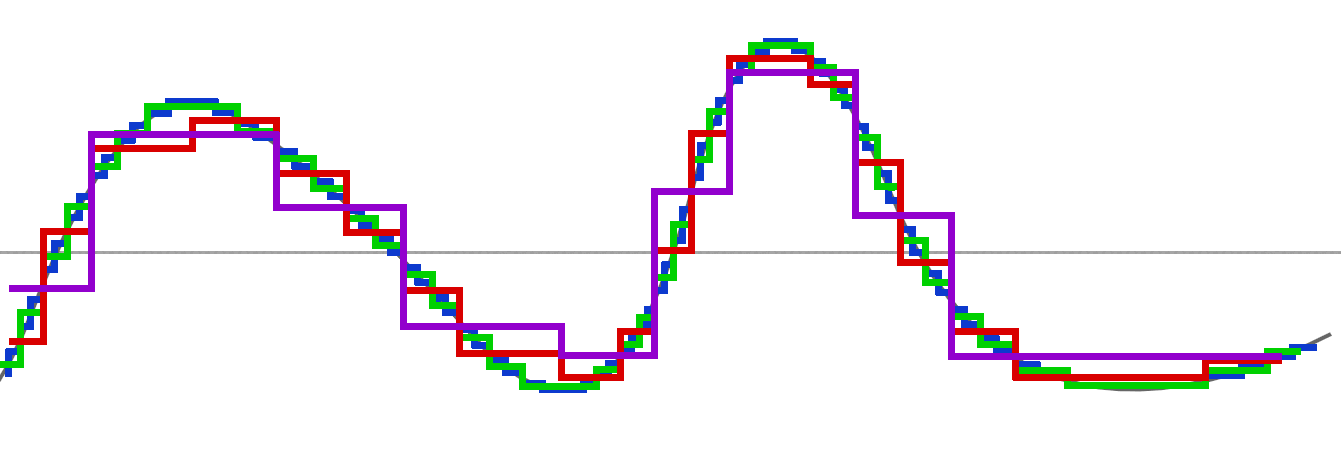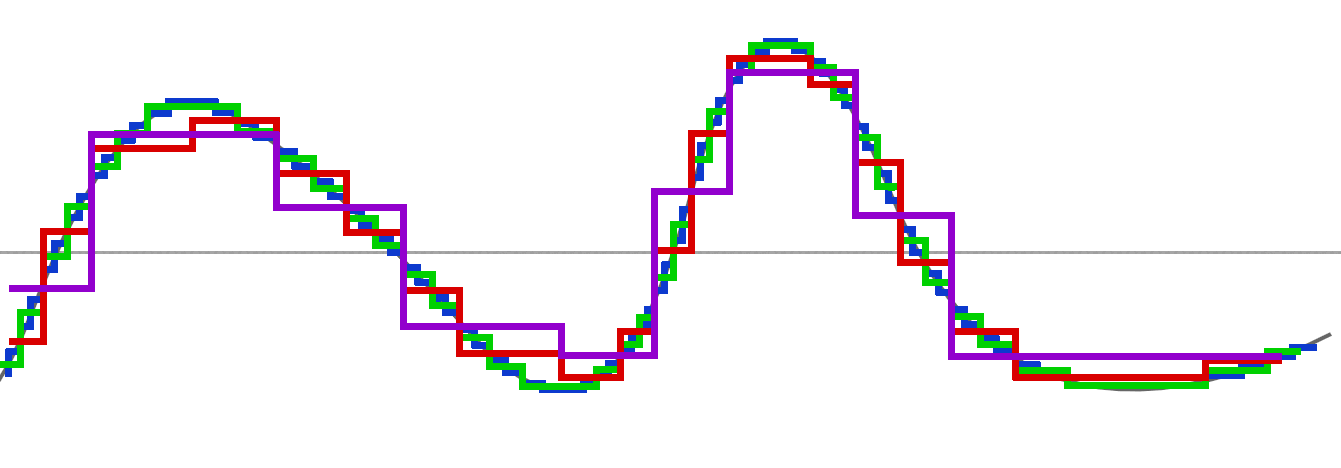
Notre version complète avec nos différents graphes combinés est (un peu) notre JPEG2000 avec ses différentes résolutions intégrées: notre JPEG2000 possèdera notre image 4K, mais aussi 2K et d'autres résolutions inférieures intermédiaires :

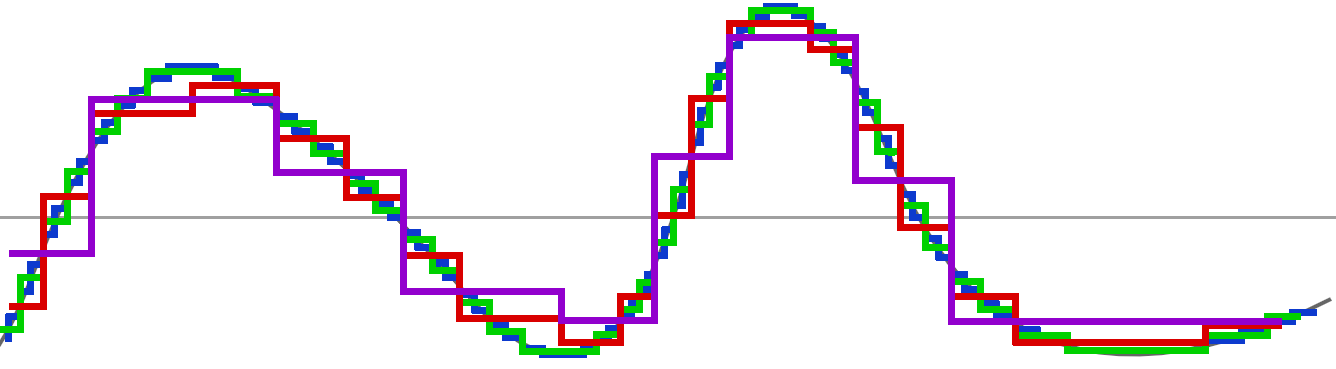
Notez que mes différentes passes peuvent être "légèrement" erronées, je n'ai pas utilisé de véritables calculs pour faire ses schémas et animations, ce n'est que pour l'exemple et que vous vous puissiez voir rapidement comment marche en partie cette compression :)

Vous me direz qu'un changement de bitdepth (passer de 16 bits à 8 bits par exemple) donneraient une résolution inférieure également, avec quasiment le même genre de résultat ? Sauf qu'avec la méthode des ondelettes, vous aurez l'ensemble des résolutions intermédiaires disponibles à tout moment et dans un seul et même flux ! (et même pouvoir avoir une résolution plus haute sur une toute petite zone en gardant le reste en basse résolution !)

Le principe des ondelettes est - entre autres - une série de calculs où nous arrivons avec des valeurs approximatives tout en conservant des valeurs intermédiaires qui nous permettent de revenir à l'original tout en conservant les résolutions intermédiaires.

Les valeurs moyennes sont appelées Coefficients d'approximations (approximation coefficients) et les valeurs de différences - donc les valeurs conservant des informations importantes pour la décomposition ou la recomposition - sont appelées Coefficients de détails (detail coefficients).

Dans nos exemples graphiques, nous voyons bien nos approximations mais il n'existe aucune valeur intermédiaire, il faut donc trouver une méthode pour conserver ces fameuses valeurs, nous allons donc voir plus en profondeur comment les calculer.

Les ondelettes par le calcul

Ce que nous allons faire maintenant, c'est calculer ces différents coefficients d'approximations et coefficients de détails.

Pour commencer, prenons une suite de valeurs pour nos données : 128, 255, 50, 100, 200, 50, 150, 255.

Dans la majorité des documentations, cette suite de données est appelée le signal. Ne vous inquiétez pas par cette terminologie. Gardez simplement que « signal = suite de données » et que - en général - on évoque le terme de signal pour les données de départ.

Ces valeurs représentent les 8 premiers pixels de notre image en noir et blanc (et en 8 bits, donc de 0 à 255). Ainsi, 0 correspond à un noir parfait, 128 à un gris et 255 un blanc absolu.

Posons nos différentes valeurs sur un graphe :

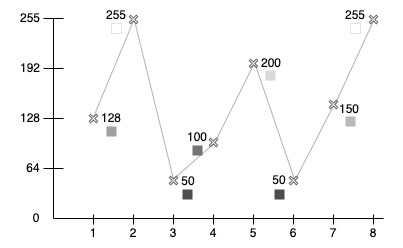
Pour débuter notre calcul en ondelettes, nous avons besoin de regrouper nos différentes valeurs par des blocs de deux unités :

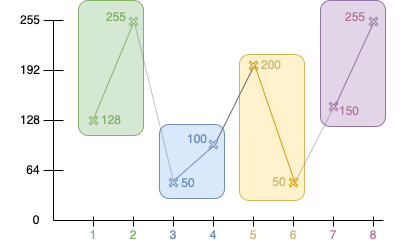
Pour calculer nos coefficients, nous devons calculer la moitié des deux valeurs pour obtenir l'approximation, et calculer afin d'obtenir la différence entre l'approximation et le chiffre secondaire du couple 4 :

Approximation   :   ( A + B ) / 2
Detail          :   ( Approx - B )      ou      ( A - B ) / 2

Si nous prenons nos deux premières valeurs :

Approximation n°1   :   ( 128 + 255 ) / 2 = 191.5

Notre premier coefficient d'approximation est donc 191.5.

Nous effectuons cela pour l'ensemble des couples de valeurs :

Approximation n°1   :   ( 128 + 255 ) / 2 = 191.5
Approximation n°2   :   (  50 + 100 ) / 2 = 75
Approximation n°3   :   ( 200 +  50 ) / 2 = 125
Approximation n°4   :   ( 150 + 255 ) / 2 = 202.5

Nos premiers coefficients d'approximations sont donc ( 191.5, 75, 125, 202.5 )

Bien entendu, nous devons aussi conserver les valeurs intermédiaires, appelés coefficient de détails.

Pour calculer le coefficient de détails, nous allons utiliser la moyenne (ou approximation) et la seconde valeur dans notre couple de valeurs [6] :

Detail n°1  :   ( 191.5 - 255 ) = -63.5         ou      ( 128 - 255 ) / 2 = -63.5
Detail n°2  :   (    75 - 100 ) = -25           ou      (  50 - 100 ) / 2 = -25
Detail n°3  :   (   125 - 50  ) =  75           ou      ( 200 -  50 ) / 2 =  75
Detail n°4  :   ( 202.5 - 255 ) = -52.5         ou      ( 150 - 255 ) / 2 = -52.5

Nos premiers coefficients de détails sont donc ( -63.5, -25, 75, -52.5 )

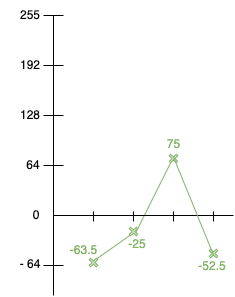
Maintenant, nous allons placer nos différentes nouvelles valeurs sur un graphe :

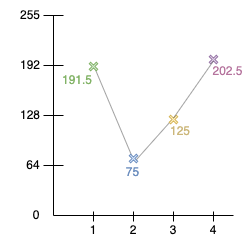
Coefficients Approximations Coefficients Détails

Ceci est notre premier niveau de décomposition !

Nos valeurs sont donc maintenant :

Approximations Details
191.5, 75, 125, 202.5 -63.5, -25, 75, -52.5

Notre but maintenant, c'est d'arriver à la plus petite base d'approximation possible.
Ici, nous constatons que nous avons encore 4 valeurs dans nos coefficients d'approximations (191.5, ...).

Nous allons passer à la seconde décomposition en ne prenant que les 4 coefficients d'approximations restants (191.5, 75, 125, 202.5), et nous allons de nouveau les regrouper par deux pour les besoins de nos calculs afin d'avoir de nouveaux coefficients approximations :

Approximation n°1   :   (191.5 + 75) / 2 = 133.25
Approximation n°2   :   (125 + 202.5 ) / 2 = 163.75

Et nous récupérons également nos coefficients de détails :

Detail n°1  :   ( 133.25 - 75 )    =  58.25         ou      ( 191.5 - 75  ) / 2 =  58.25
Detail n°2  :   ( 163.75 - 202.5 ) = -38.75         ou      ( 125 - 202.5 ) / 2 = -38.75

Et plaçons-les de nouveau dans un graphe :

Coefficients Approximations Coefficients Détails

Nos nouvelles valeurs de décomposition pour ce niveau sont donc :

Approximations Details
133.25, 163.75 58.25, 38.75

Avec nos dernières valeurs d'approximations, pouvons-nous encore décomposer ?
Bien évidemment, nous avons encore un couple de valeurs (133.25, 163.75) que nous pouvons de nouveau décomposer :

Approximation n°1   :   (133.25 + 163.75) / 2 = 148.5

Et notre coefficient de détail :

Detail n°1  :   (148.5 - 163.75) = -15.25           ou      (133.25 - 163.75) / 2 = -15.25

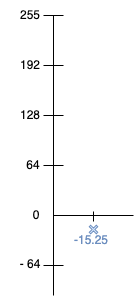
Et de nouveau sur un graphe :

Coefficients Approximations Coefficients Détails

Nous n'avons plus de couple de coefficients d'approximations, il ne reste plus qu'une valeur dans notre approximation, nous pouvons donc nous arrêter :

Approximations Details
148.5 -15.25

Vous ne remarquez pas quelque chose ? Notre graphe de coefficients d'approximations ne contient plus qu'une seule valeur, alors qu'au début, nous avions 8 valeurs. Nous venons de compresser (indirectement) notre signal !

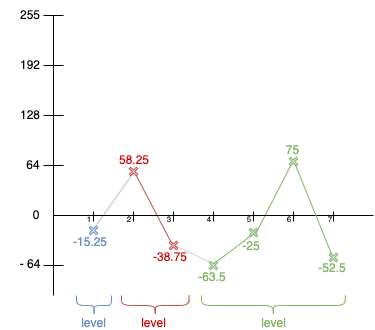
Lorsque nous arrivons à ne plus pouvoir décomposer, nous avons maintenant notre décomposition totale en intégrant notre coefficient d'approximation et nos différents coefficients de détails que nous avons calculés dans les différentes étapes de notre décomposition :

Coefficient Approximation Coefficients Détails

Car oui, il est important de conserver les différents coefficients de détail que nous avons calculé aux différentes étapes. Les autres coefficients d'approximations peuvent être oubliés, on ne conservera que le dernier, l'unique. C'est par lui que nous pouvons - et à l'aide des différents coefficients de détails - reconstruire les autres coefficients d'approximations des différents niveaux.

L'avantage de cette méthode, c'est que nous avons - dans un seul signal - l'ensemble des résolutions possibles !

Voici ce que nous avons fait en une seule image :

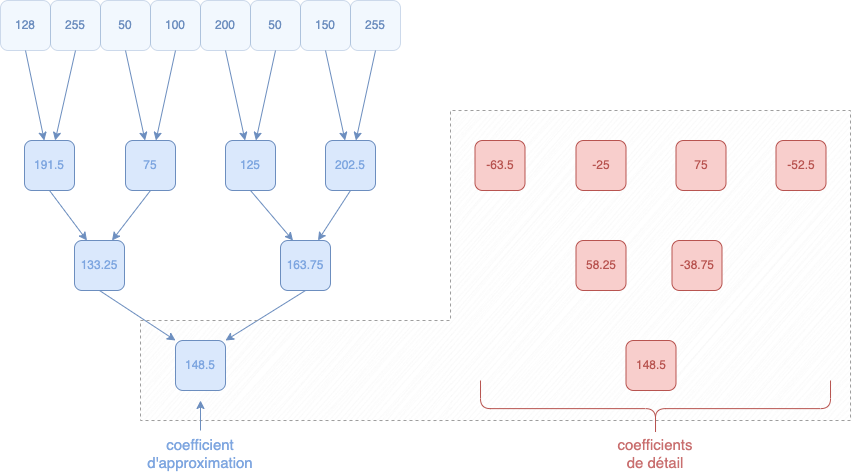
À la fin, nous arrivons donc avec 1 seul coefficient d'approximation et 7 coefficients de détail.

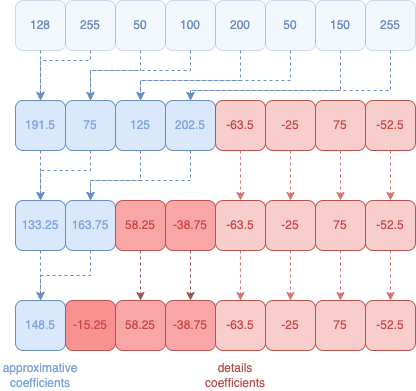
Visuellement, voici la cascade de nos différents calculs et la conservation des coefficients de détail à travers les différents niveaux de décomposition :

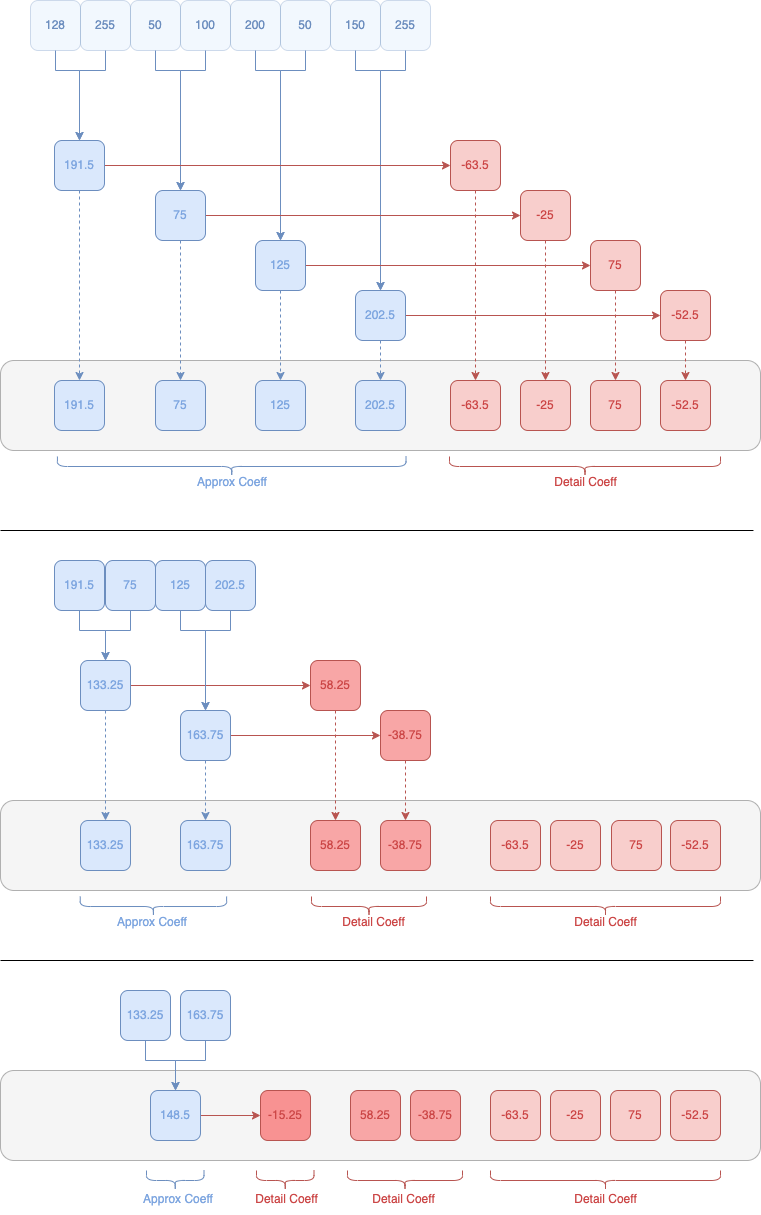
Chaque groupe de coefficients de détail représentent un niveau de décomposition qui va nous permettre de retrouver l'ensemble de nos niveaux de décomposition, nos différentes résolutions.

De manière simplifiée, nous avons effectué cette boucle jusqu'à ne plus avoir de données à décomposer, tout en mettant de côté les coefficients de détails :

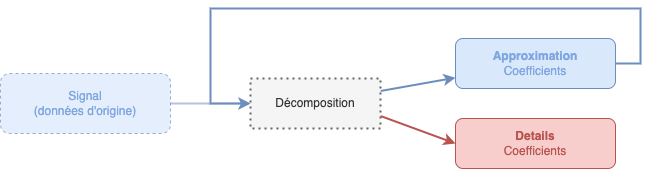
À chaque fois que nous passons par le bloc de décomposition, nous passons à un nouveau niveau de résolution.

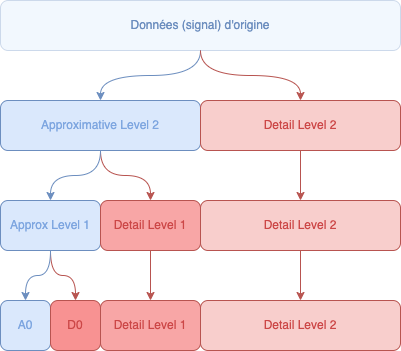
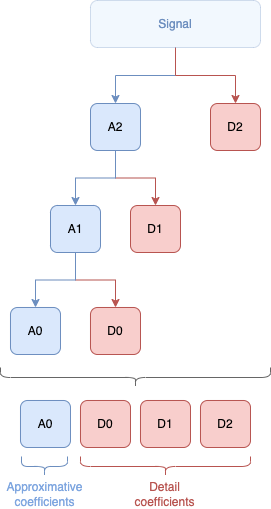
À chaque niveau de décomposition, nous conservons les coefficients de détails précédents. À l'aide de ces schémas représentant nos précédents calculs, nous voyons les différentes étapes de la décomposition totale :

Schéma en étage Schéma en arbre Schéma chiffré

Vous retrouverez un petit programme en Python - écrit à l'arrache - en utilisant cette décomposition simple 1D pour vous amuser :

# ./wavelet_base_1D.fromscratch.py
Using Wavelet 1/2

input=[128, 255, 50, 100, 200, 50, 150, 255]

================= 1st decomposition ==================================
191.5, 75.0, 125.0, 202.5       -63.5, -25.0, 75.0, -52.5
'------- approx --------'       '---- detail ------------'

================= 2nd decomposition ==================================
133.25, 163.75      58.25, -38.75, -63.5, -25.0, 75.0, -52.5
'-- approx --'      '-------------- detail -----------------'

================= 3rd decomposition ==================================
148.5       -15.25, 58.25, -38.75, -63.5, -25.0, 75.0, -52.5
'-A-'       '-------------------- detail ------------------'

Dans ce paragraphe, notre exemple était une simple décomposition 1D avec très peu de données et sans utiliser l'ensemble des paramètres et fonctions constituant les ondelettes. Dans l'ensemble, si vous avez déjà compris cette vulgarisation, vous avez une idée générale et très simplifiée de la base du concept des ondelettes.

Pour résumer, le coefficient d'approximation est le coeur de notre structure, on le surnomme parfois "énergie" car c'est par lui - ce point de départ - et à l'aide des différents coefficients de détail - que nous pourrons reconstruire les différentes données aux différents paliers (ou résolutions) et à la fin, reconstruire les données d'origine.

Notez ici que je ne parle que d'un coefficient d'approximation, mais selon la quantité de données et le niveau de décomposition, nous aurons une multitude de coefficients d'approximation.

Les autres familles d'ondelettes (Haar, Daubechies, ...) intègrent des fonctions de scaling, des fonctions de wavelet, des coefficients de filtrage passe-bas et filtrage passe-haut (filter low-pass, filter high-pass) - dont les coefficients peuvent parfois être différents à certaines étapes, en 1D, en 2D et aussi en 3D. Elles sont un peu plus complexes mais l'idée générale est la même.

Maintenant que nous avons vu une décomposition simple 1D, voyons une décomposition simple en 2D.

Les décompositions 2D - pour les images

Précédemment, nous avons vu une décomposition en 1D et nous avions besoin d'au moins 2 valeurs.

Maintenant, avec une décomposition en 2D, nous avons un doublement des valeurs, nous aurons donc 2x2 valeurs. Ce bloc de données est appelé une matrice :

Nous allons appliquer des calculs sur cette matrice de 4 valeurs. Tout comme notre décomposition en 1D (2 valeurs) qui générait une décomposition avec 2 autres valeurs (1 approximation + 1 détail), notre matrice de départ en 2D va générer une matrice de décomposition en 2D :

Vous remarquerez que dans la matrice de coefficients, nous avons deux différentes lettres - A et D - qui représentent respectivement notre coefficient d'approximation et nos coefficients de détail.

Nous allons voir maintenant, avec nos données en 2D, comment nous allons arriver à nos différents coefficients. Pour cela, nous allons devoir appliquer notre méthode de calcul pour un environnement en 2D :

A l'aide des valeurs a, b, c et d, nous allons produire une valeur d'approximation (A) pour l'ensemble du bloc et également trois valeurs de détail (D).

L'ensemble de ces valeurs sont surnommés respectivement LL, HL, LH et HH. Ces blocs sont appelés sous-bandes ou subbands.

Acronyme Description Nom
LL Low-Low Resolution - Approximation - Basse Résolution Approximation
HL High vertical resolution / Low horizontal resolution Details Verticaux
LH Low vertical resolution / High horizontal resolution Details Horizontaux
HH High-High Resolution Details Diagonaux

Vous retrouverez beaucoup ces acronymes et noms dans les différentes documentations sur le JPEG2000.

Notez que - selon les implémentations - LL, HL, LH et HH peuvent se retrouver à différents endroits, dont voici les principales dispositions les plus couramment observées :

Dans le cadre du JPEG2000, nous serons dans cette disposition :

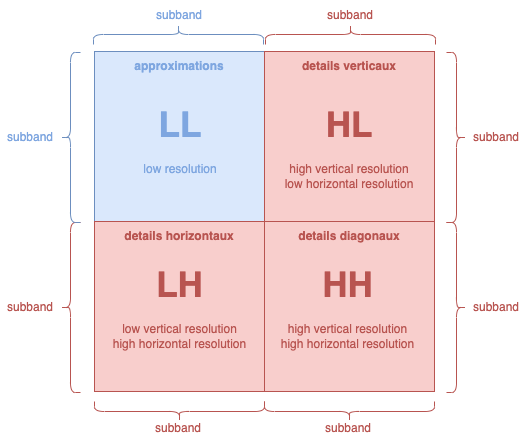
Dans le cadre de notre chapitre, nous utiliserons cette disposition et une inversion entre HL et LH également (juste parce que certains programmes et librairies l'utilisent, mais le JPEG2000 reste avec un HL à droite).

Pour calculer les différents coefficients, voici les différentes équations possibles pour obtenir LL, LH, HL et HH :

Zone Calcul Représentation graphique
LL
(Approximation) 		( (a+b) + (c+d) ) / 2
LH
(Detail Horizontal) 		( (a+b) - (c+d) ) / 2
HL
(Detail Vertical) 		( (a+c) - (b+d) ) / 2
HH
(Detail Diagonal) 		( (a-b) - (c-d) ) / 2

Pour LL (Approximation), rien de bien compliqué, comme pour la version 1D, nous additionnons toutes les valeurs et divisons par 2 pour obtenir une valeur moyenne.

Pour LH (Detail Horizontal), nous allons additionner les deux valeurs horizontalement, les soustraitent entre elles.

Pour HL (Detail Vertical), nous effectuons l'exact opposé de l'équation LH : nous allons additionner les deux valeurs verticalement.

Pour HH (Detail Diagonal), l'équation est l'exact opposé de l'équation pour LL, nous allons tout soustraire.

À partir de là, on va calculer chaque bloc de 2x2 de nos données, et placer les résultats dans les subbands LL, HL, LH ou HH (les sens et les emplacements peuvent changer entre HL et LH). Ici, nous avons neufs blocs de 2x2 pour notre exemple :

À la fin, nous aurons cette nouvelle matrice :

Cette matrice est notre premier niveau de décomposition :

Nous pouvons continuer à décomposer afin d'obtenir une hiérarchie comme telle :

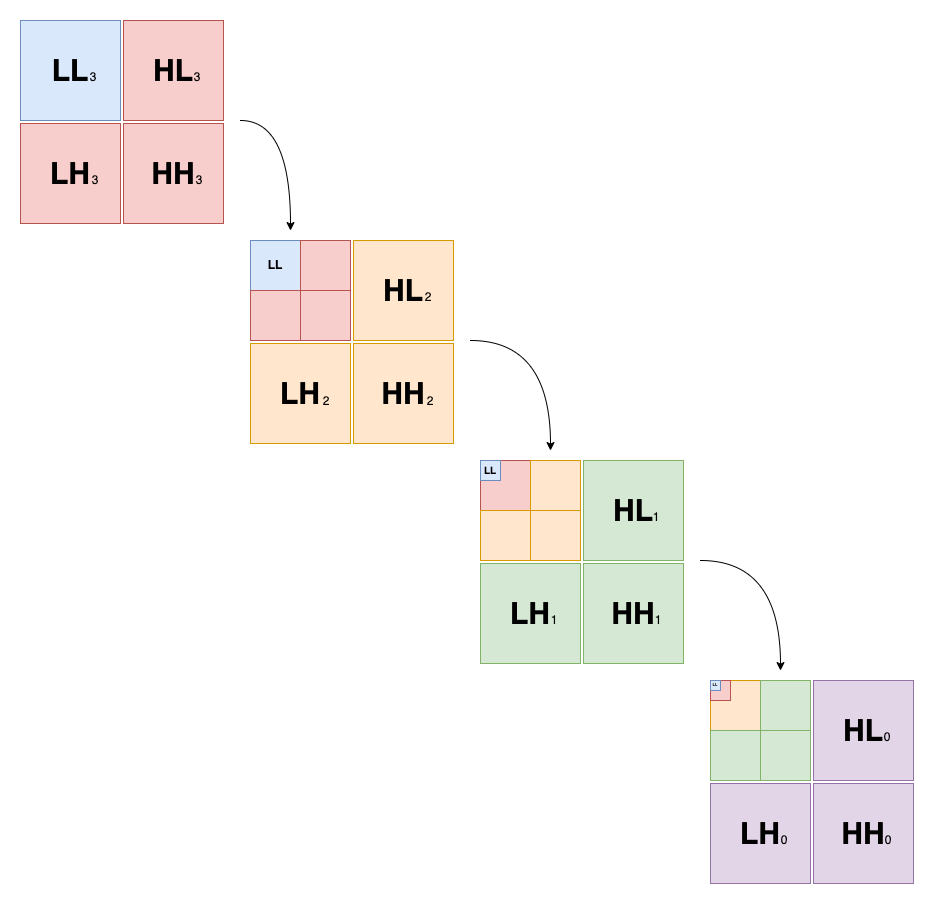
Chaque nouvelle décomposition devient le nouveau LL pour la prochaine étape. Attention, le LL d'un niveau n'est pas conservé dans l'image finale, on ne conservera que le tout-petit LL final.

Voyons les différentes étapes une à une :

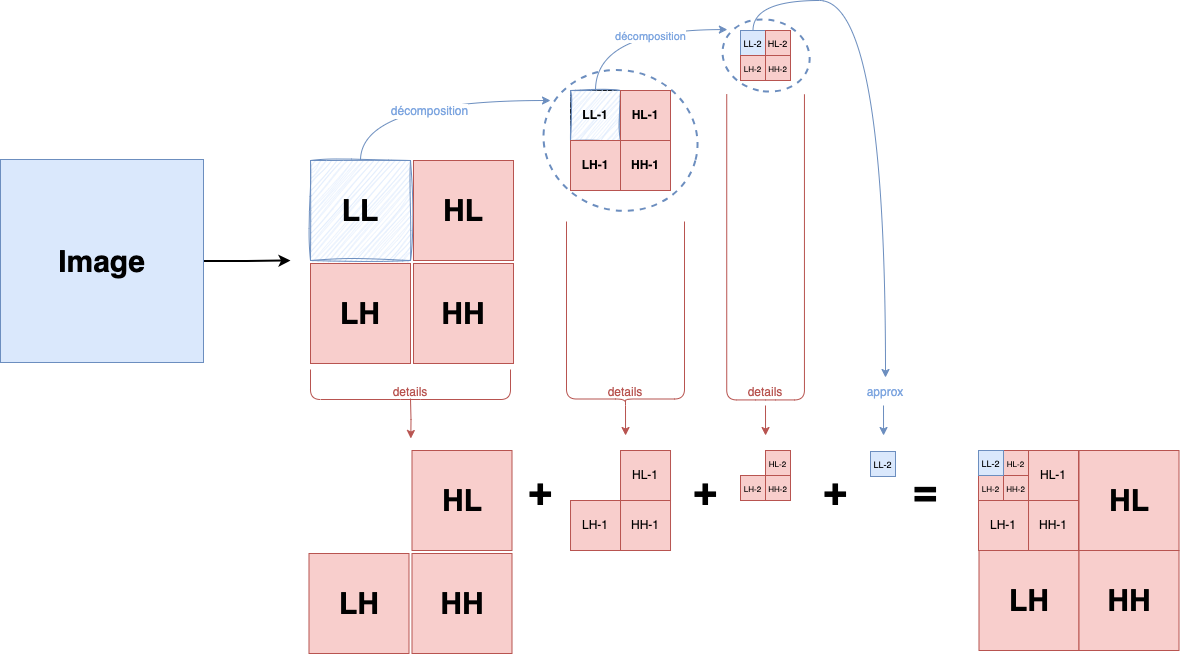
Nous partons de notre image, on va décomposer pour obtenir les subbands LL, HL, LH et HH. On va conserver les subbands de détails à part et on va de nouveau décomposer ce LL en d'autres subbands de details (HL-1, LH-1, HH-1) et avec le LL-1 (coefficient approximation), nous effectuons une nouvelle décomposition pour obtenir les subbands de details HL-2, LH-2, HH-2 et on aura enfin un LL-2 (coefficient approximation). Nous prenons l'ensemble de nos details et nous ne conservons que le dernier LL (LL-2) pour créer notre image waveletisée.

À la fin, nous obtiendrons un résultat de la sorte :

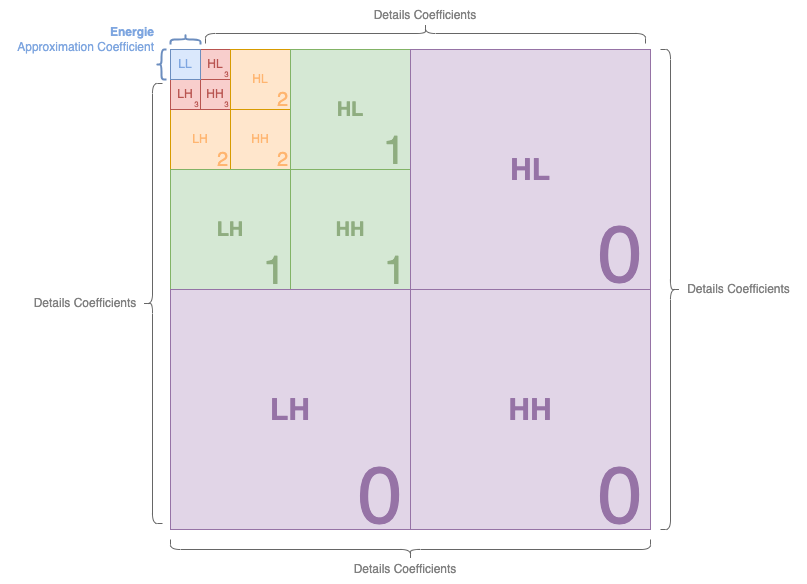
Avec une image, nous obtiendrons ceci :

Votre JPEG2000 ressemblera à une suite de subbands (LL, HL, LH, HH) en cascade dont chaque niveau représente une nouvelle résolution.

Et étape par étape :


Si vous voulez vous amuser, un programme (aussi écrit rapidement, le but étant de comprendre sans avoir une masse de code) vous permet d'effectuer un premier niveau de décomposition en 2D (seulement une matrice 2x2) :

# ./wavelet_haar_2D.py

====== Signal ======
[15, 35]
[45, 75]

  -------------------
  |        |        |
  |  A/LL  |  H/LH  |
  |        |        |
  -------------------
  |        |        |
  |  V/HL  |  D/HH  |
  |        |        |
  -------------------

====== From pywt ======
LL : 85.000000
LH : -35.000000
HL : -25.000000
HH : 5.000000

====== From scratch ======
LL : 85.000000
LH : -35.000000
HL : -25.000000
HH : 5.000000

Ainsi qu'un programme pour générer les différentes images représentant LL, HL, LH et HH :

Using external data from data.gray.png

Display input data
 0.14117648 0.14117648 0.13725491 0.13725491 0.13725491 0.13725491
 0.14901961 0.14509805 0.14117648 0.14117648 0.14117648 0.13725491
 (...)
 
Display wavelet output
LL=
    [ 0.27254903 0.26862746 0.27254903 ... 0.07647058 0.0490196  0.01960784 ]   ...
    [ 0.00784314 0.00784314 0.00784314 ... 0.00784314 0.00784314  0.00784314 ]  ...

LH=
    [ 0.00980392  0.00588236  0.00196079 ... -0.00588235  0.01372549  0.00784314]   ...
    [ 0.          0.          0.         ...  0.          0.          0.        ]   ...

HL=
    [ 1.9607693e-03 -1.9607842e-03 -1.9607842e-03 ...  5.8823489e-03  5.8823526e-03  7.8431368e-03 ] ...
    [ 0.0000000e+00  0.0000000e+00  0.0000000e+00 ...  0.0000000e+00  0.0000000e+00  0.0000000e+00 ] ...

HH=
    [ 1.9607879e-03  5.1222742e-09  3.9215693e-03 ...  1.9607833e-03  1.9607847e-03  5.8823526e-03 ] ...
    [ 0.0000000e+00  0.0000000e+00  0.0000000e+00 ...  0.0000000e+00  0.0000000e+00  0.0000000e+00 ] ...

Save wavelet output to png

A partir de votre image d'entrée (en noir & blanc), vous obtiendrez 3 images pour LL, LH, HL, et HH.

Les fonctions et filtrages

Si vous vous souvenez, nous évoquions rapidement l'utilisation de « fonctions », « filtrages » et autres « downscaling ».

Les ondelettes utilisent deux types de "fonctions" : Scaling et Wavelet. Les deux travaillent de pair pour décomposer ou recomposer une image et travaillent chacune à un certains moments pour générer un certain type de données :

Nom de la fonction Surnom Type d'output Utilisation Code Symbole
Scaling Function Father Approximative Coefficient Filtre Passe-Bas L φ
Wavelet Function Mother Detail Coefficient Filtre Passe-Haut H ψ

Ces éléments, nous les avons déjà vu dans les paragraphes suivants ... mais ils étaient tellement bien cachés que vous êtes passés par-dessus, mais vous les avez bien vu :-) :

Si nous développons un peu la partie "Décomposition", nous trouverons nos différents éléments :

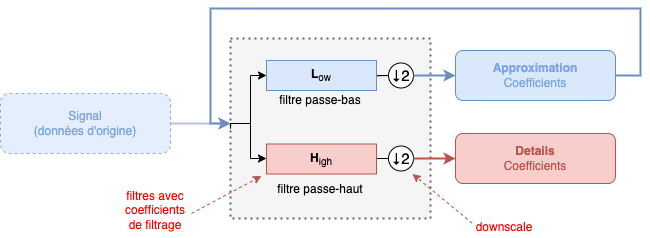
Quand nous calculions la moyenne de deux valeurs pour avoir le coefficient d'approximation, nous jouions avec la Scaling Function (Filtre Passe-Bas). Quand nous calculions la différence pour obtenir le coefficient de détail, nous jouions avec la Wavelet Function (Filtre Passe-Haut). Le downscaling étant intégré (dans notre exemple) dans le tout via sa division par deux.

Notez que la séparation - entre Low et High - ne réprésente pas une division par deux de notre signal, mais seulement que le même signal va passer autant dans Low que dans High. Par exemple, si notre signal a une valeur de 1, ce chiffre va passer dans Low et dans High.

Voici l'exemple du workflow complet d'une seule décomposition en 2D sur des données d'une image, et comment s'articulent les différentes passes de décomposition avec les différents filtres et downscaling (⇣2) :

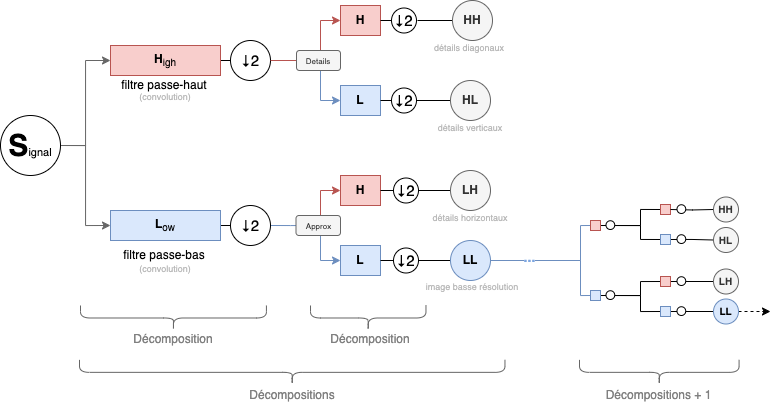
Les filtres "high-pass" coupent les basses fréquences. Les filtres "low-pass" coupent les hautes fréquences. Dit indirectement, les high-pass conservent les hautes-fréquences et les low-pass conservent les basses-fréquences.

Concrètement, nous passons nos données dans notre filtre low-pass, nous obtenons nos coefficients d'approximations. Et avec le même input, nous le passons dans notre filtre high-pass et nous obtenons nos coefficients de détails.

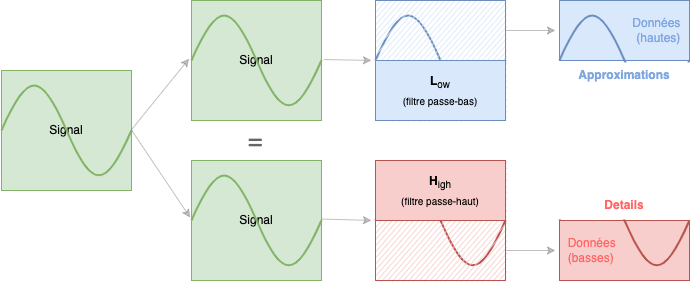Les approximations ne conservent que l'énergie haute, il faut donc un filtre passe-bas pour supprimer (couper) l'énergie basse pour ne conserver que l'énergie haute.
Les details ne conservent que l'énergie basse, il faut donc un filtre passe-haut pour supprimer (couper) l'énergie haute et ne conserver que l'énergie basse.

La première phase est notre première résolution. Dès que nous avons réussi à générer le LL d'une résolution plus basse, nous recommençons sa décomposition pour produire une résolution plus basse encore, et ainsi de suite.

Pour comprendre le choix des acronymes LL, LH, HL et HH, il suffit d'entourer les bonnes cases des filtres :)

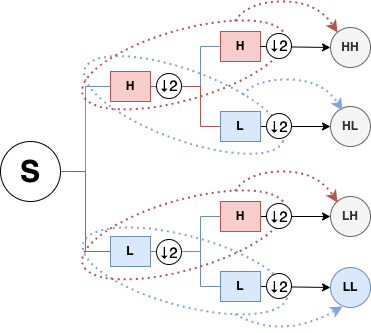
Avec une image, voyons concrètement les transformations effectuées :

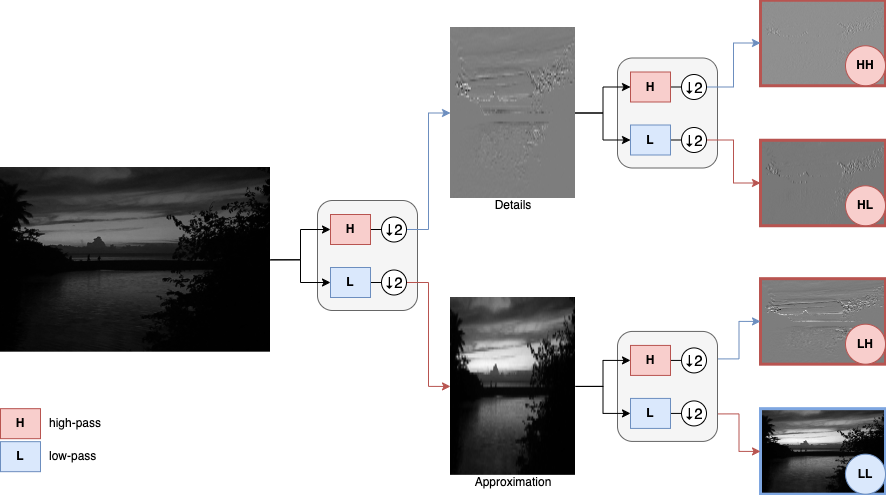
Avec notre petite équation, notre décomposition est relativement simple. Cependant, avec les autres familles d'ondelettes, l'équation de filtrage devient un peu plus compliquée. Les équations deviennent plus complexes car elles intègrent des coefficients de filtrages plus complexes, plus longs.

Pour comprendre le concept des coefficients de filtrages, voyons cela dans le paragraphe suivant.

Les sub-bands LL, HL, LH & HH

Revenons un petit moment sur les termes LL, HL, LH et HH représentant les différents subbands que nous retrouverons dans notre encodage JPEG2000.

Dans plusieurs documentations, pour parler les subbands LL, HL, LH et HH, on va vous parler de Horizontal Low-pass filter, Vertical High-pass filter, Vertical Details, Horizontal Details, etc... Dans le flot, vous pouvez être perdu. Et cela serait totalement compréhensible vu le peu d'explication trouvable qui font liens entre tous ces termes.

Pour bien comprendre le lien entre eux, nous allons visualiser les différents types de subbands par type de filtrage et leurs résultats en sortie de filtres :

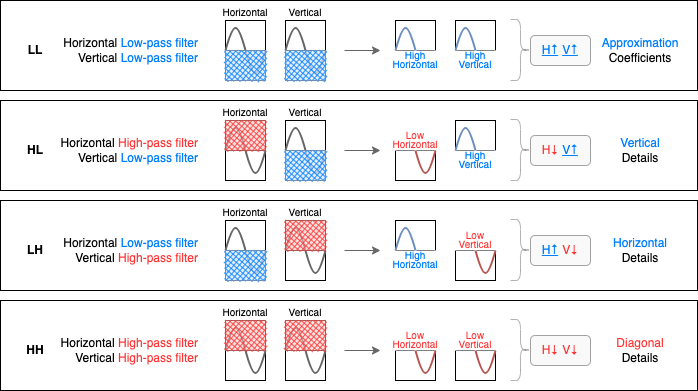
Les lettres H et L représente respectivement les mots High et Low. Ils sont dans un certain ordre (HH ou HL ou LH ou LL) car ils indiquent le type de filtre que nous allons appliquer respectivement sur les données en Horizontal et en Vertical.

Ainsi, le HL a un filtre Horizontal High-pass et un filtre Vertical Low-pass, et contrairement à ce que le mot pass laisse supposer, ils ne laissent pas du tout passer, ils filtrent :

En sortie, nous n'aurons plus que des données basses pour l'Horizontal et des données hautes pour le Vertical. Notre HL en sortie de filtre représente surtout des données verticales car ce sont les seules données qui seront hautes en sortie de filtres.

Voici un tableau récapitulatif entre les différents subbands :

Name Filtering Resolution Wavelet Coefficients Type
LL Low - Low Horizontal Low-pass filter
Vertical Low-pass filter		 High Horizontal Resolution
High Vertical Resolution		 Approximation
HL High - Low Horizontal High-pass filter
Vertical Low-pass filter		 Low Horizontal Resolution
High Vertical Resolution		 Vertical Details
LH Low - High Horizontal Low-pass filter
Vertical High-pass filter		 High Horizontal Resolution
Low Vertical Resolution		 Horizontal Details
HH High - High Horizontal High-pass filter
Vertical High-pass filter		 Low Horizontal Resolution
Low Vertical Resolution		 Diagonal Details

Les coefficients de filtrages (filter banks)

Pour comprendre le lien entre le filtre et ses coefficients, c'est - toute raison gardée - la même qu'une console de jeux-vidéo et les cartouches qu'on y insère. La console étant le filtre et la cartouche étant les coefficients. La cartouche va "transformer" le comportement de la console et afficher différents éléments. Les coefficients de filtrage jouent un peu le même rôle, ils vont influencer les filtres passe-haut et passe-bas.

Les coefficients de filtrages sont les éléments importants des ondelettes, elles seront intégrées dans les blocs - des filtres - "high-pass" et "low-pass".

Dans notre premier exemple, les filtres passe-bas et passe-haut sont relativement simples :

    Approx = L(ow)  = ( A + B ) / 2   <-- low-pass
    Detail = H(igh) = ( A - B ) / 2   <-- high-pass
                      '---.---'  '-'
                          |       |
                   low/high-pass  '-- downscaling ↓

Dans ce dernier, nous n'avons pas de coefficient de filtrage (sauf si on considère que notre coefficient de filtrage est de 1 :)

Par exemple, l'ondelette de type "Haar" (la forme la plus simple des ondelettes) utilise comme coefficient de filtrage passe-bas et passe-haut, la racine carrée de 2 :

    Approx = ( (A + B) * sqrt(2) ) / 2   <-- low-pass
    Detail = ( (A - B) * sqrt(2) ) / 2   <-- high-pass
             '---------.----|----'  '-'
                       |    |        |
             low/high-pass  |        '-- downscaling ↓
                            |
                      coeff. filter

Avec les autres familles, les coefficients de filtrages deviennent beaucoup plus complexes et nous aurons des équations plus longues.

Différents calculs pour le même résultat

Sur de nombreux sites évoquant les wavelets, dans les bases de données, dans les programmes ou même les librairies, les coefficients sont très souvent réduits sous une forme simple d'une suite de chiffres (qui semblent n'avoir pas beaucoup de sens sans l'équation de base).

Par exemple, avec l'ondelette de Haar, au lieu d'intégrer une équation avec le calcul de sa racine-carré, nous pourrons retrouver un simple 0.70710678118654752440 pouvant être décliné sous différents aspects :

Cette utilisation particulière de la racine-carré de 2 s'explique par le fait d'intégrer directement le downscaling (⇣2) dans l'équation. On va diviser directement la racine-carré de 2 par 2. Avec cette astuce, il nous suffit plus que d'appliquer ce chiffre à notre valeur de données.

Ainsi, si nous devions appliquer un filtre passe-haut à une valeur de données « 5 », toutes ces équations sont équivalentes :

Vous pourrez donc trouver sur certains endroits, différentes implémentations des différentes équations des filtres, selon l'humeur de l'auteur :)

Cela garde un intérêt durant les phases de calcul, il est plus simple pour un ordinateur de faire de simples calculs de base (multiplication, addition, soustraction) que de se faire à chaque fois tous les calculs des équations complexes.

N'oubliez jamais que certains coefficients peuvent prendre en compte un petit sqrt(2) dans leurs équations afin d'obtenir leurs valeurs finales. Cette utilisation de sqrt(2) est appelée normalisation des outputs.

Petits calculs et grands coefficients

Maintenant que nous avons vu rapidement le principe des coefficients de filtrages, nous allons essayer d'effectuer un calcul avec la wavelet Daubechies-2.

Pourquoi Daubechies-2

Pourquoi ne pas commencer par Daubechies-1 ? Tout simplement parce que nous l'avons déjà vu :)

Si vous regardez les wavelets et coefficients Db1, cela vous dira déjà quelque chose. Dans les coefficients, nous avons 0.7071067, qui est le résultat de 1 * 1/sqrt(2). Et avec un coefficient de 1, c'est notre premier exemple mais avec une normalisation en plus (sqrt(2)).

Pour construire nos filtres high-pass et low-pass, on va avoir besoin de nos coefficients de filtrages pour chacun.

Sur le site Wavelet Browser, nous avons ces 8 coefficients pour la décomposition :

Low-pass High-pass
-0.1294095226 -0.4829629131
0.2241438680 0.8365163037
0.8365163037 -0.2241438680
0.4829629131 -0.1294095226

4 coefficients pour notre filtre low-pass,
4 coefficients pour notre filtre high-pass

N'oubliez pas que les coefficients de filtrage ne sont que les résultats finaux d'équations plus ou moins complexes.

Pour Db-2, voici l'équation complète, avec en complément les calculs avec la normalisation 1/sqrt(2) (à votre droite) :

Les autres wavelets sont beaucoup plus complexes, ne gardez que les coefficients finaux pour vos calculs.

Nous pouvons également récupérer ces coefficients via pywt :

import pywt
wavelet = pywt.Wavelet("db2")

# Low-pass (decomposition)
print(*wavelet.dec_lo)
-0.12940952255126037 0.2241438680420134 0.8365163037378079 0.48296291314453416

# High-pass (decomposition)
print(*wavelet.dec_hi)
-0.48296291314453416 0.8365163037378079 -0.2241438680420134 -0.12940952255126037

Vous trouverez également l'ensemble des coefficients de beaucoup de famille d'ondelettes dans ce fichier ou à cette adresse (X)

Sur certaines documentations, vous trouvez également ces valeurs :

-0.1830127, 0.3169873, 1.1830127, 0.6830127

Si c'est le cas, ne paniquez pas, vos coefficients ne sont pas faux, c'est qu'ils intègrent déjà le facteur de normalisation - toujours notre fameux sqrt(2) - et si nous enlevons notre normalisation via un 1/sqrt(2), nous retrouvons les chiffres données par Wavelet Browser et pywt :

-0.1830127 * 1/sqrt(2) = -0.12940952121325926611
 0.3169873 * 1/sqrt(2) =  0.22414386938001449608
 1.1830127 * 1/sqrt(2) =  0.83651630239980679052
 0.6830127 * 1/sqrt(2) =  0.48296291180653302831

Avec pywt, vous retrouverez ces valeurs sous les variables scaling et wavelet :

import pywt

wavelet = pywt.Wavelet("db2")
(phi, psi, x) = wavelet.wavefun(level=1)

# phi = Scaling function
print("Scaling function:", *phi)
Scaling function: 0.0
                  0.6830127018922194  
                  1.1830127018922194 
                  0.3169872981077807 
                 -0.18301270189221933 
                  0.0 
                  0.0

# psi = Wavelet function
print("Wavelet function:", *psi)
Wavelet function: 0.0
                 -0.18301270189221933
                 -0.3169872981077807
                  1.1830127018922194
                 -0.6830127018922194 
                  0.0 
                  0.0

Avant de nous lancer la tête la première dans des calculs, débutons notre décomposition en nous basant sur deux méthodes déjà établies : pywt et numpy.

Avec pywt, tout est relativement simple, il suffit de nos données d'entrée (signal) et de définir le type d'ondelette utilisée (db2), pywt se chargera de calculer tout ce qu'il faut pour arriver à la première décomposition à l'aide de dwt() : 

import pywt
signal = [1, 20, 3, 40]
coeffs = pywt.dwt(signal, 'db2')
print(*coeffs)
[  8.13172798,  12.70933969,  43.48706704]      <== coefficients approximations Db2
[-11.63507628, -21.4212545 ,  22.65778012]      <== coefficients details Db2

Et voilà, nous avons notre première décomposition avec Daubechies-2 !

Maintenant, essayons avec numpy, nous pourrons voir les différentes étapes, la convolution (calcul de deux vecteurs), le downscale et la suppression des bordures des données de sortie :

import numpy as np # nos données signal = [1, 20, 3, 40] # nos coefficients Db2 - High-pass wavelet_dec_hi = [-0.48296291314453416, 0.8365163037378079, -0.2241438680420134, -0.12940952255126037] # nos coefficients Db2 - Low-pass wavelet_dec_lo = [-0.12940952255126037, 0.2241438680420134, 0.8365163037378079, 0.48296291314453416]
# convolution du signal et coefficients low-pass # On calcule les coefficients d'approximation approximations = np.convolve( signal, wavelet_dec_lo, "valid" ) print("convolution:", *approximations) # downscale approximations = approximations[::2] print("downscale:", *approximations) # remove extra output (final output) approximations = approximations[1:-1] print("clean:", *approximations) # convolution du signal et coefficients high-pass # On calcule les coefficients de détail details = np.convolve( signal, wavelet_dec_hi, "valid" ) print("convolution:", *details) # downscale details = details[::2] print("downscale:", *details) # remove extra output (final output) details = details[1:-1] print("clean:", *details)
convolution: 12.70933969 downscale: 12.70933969 clean: 12.70933969 convolution: -21.4212545 downscale: -21.4212545 clean : -21.4212545
Approximations Details

Et là... c'est le drame, nos valeurs de fin avec numpy ne sont pas les mêmes qu'avec pywt. Si nous regardons bien, nous n'avons que 2 valeurs en commun avec la sortie de pywt. Pourquoi ?

Il faut comprendre un petit principe : avec 4 coefficients de filtrage, nous devons les appliquer avec 4 valeurs de données et pour chacune des données de notre signal.

Je m'explique : nos 4 coefficients de filtrage vont s'appliquer sur nos 4 valeurs afin d'obtenir la première valeur de notre calcul. Mais ce dernier est en rapport avec notre première valeur d'input (ici 1).

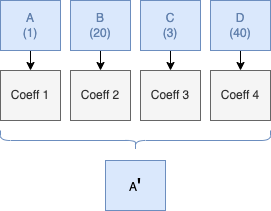
Après ce calcul, nous devons donc appliquer ce même mécanisme pour le nombre suivant dans nos données d'entrées (ici 20), donc on va décaler nos données vers la gauche, et ainsi de suite jusqu'à la dernière donnée de notre signal (40).

Cependant, nous avons un souci : si nous décalons nos données, sur quelles données les 4 coefficients de filtrage vont-t-ils s'appliquer en bout de chaîne ?

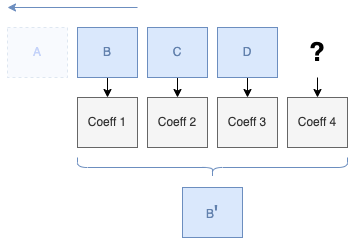
Et c'est là que le principe du padding intervient.

Dans les calculs par ondelettes, si nous n'avons pas assez de données pour appliquer les différents coefficients, nous pouvons appliquer un complément de données appelé padding. Vous avez plusieurs formes de padding :

Nom Description
Zero Padding On rajoute des 0
Constant Padding Les données en bordures sont utilisés comme valeur de référence pour le padding
Symmetric Padding Effet miroir des données initiaux
Reflect Padding Réflexion des données
Periodic Padding Une sorte de replica des données
Smooth Padding Le signal est étendu suivant les premiers calculs
Antisymmetric Padding La même que symmetric mais avec des valeurs négatives
Antireflect Padding Fusion de la méthode antisymmetric et reflect.

Vous trouverez de plus amples informations à propos des différents paddings sur cette page.

Par défaut, pywt utilise la méthode symmetric et effectue ce travail de padding automatiquement (via l'option mode), c'est à dire qu'il va utiliser les données de votre signal et les répliquer en sens inverse avant de procéder aux différents calculs nécessaires.

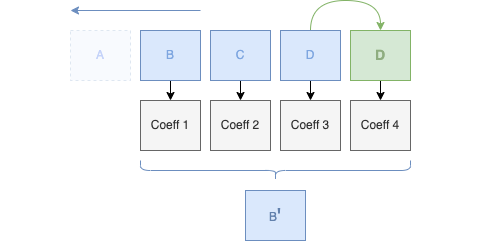
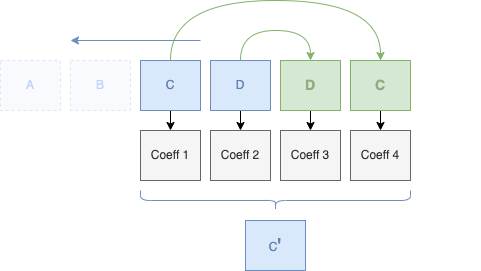
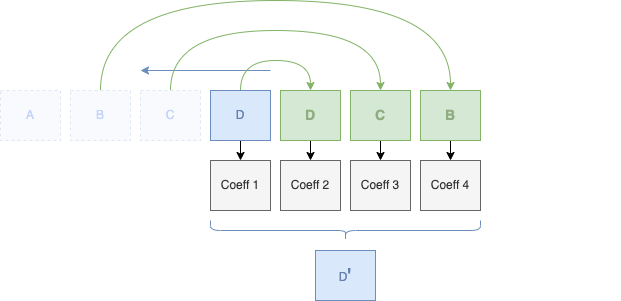
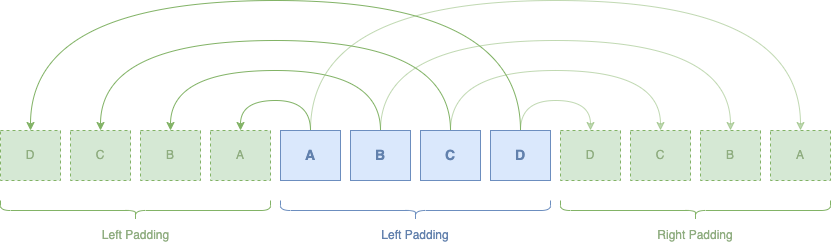
Notre signal [A, B, C, D] va être complété du côté droit ainsi [A, B, C, D, D, C, B, A]. Vous voyez qu'on ne fait que répliquer nos données comme dans un miroir. Cependant, il faut aussi appliquer le même principe du côté gauche. Ainsi, notre signal va devenir au final [D, C, B, A, A, B, C, D, D, C, B, A] :

Intégrons maintenant notre nouveau signal avec son padding (en vert) dans notre précédent programme :

# padded signal - symmetric signal = [40, 3, 20, 1] + [1, 20, 3, 40] + [40, 3, 20, 1] # |____________| |____________| # |________________________________| # | # symmetric padding
( ... calcul ... )
convolution: 26.18153328 18.27394916 8.13172798 5.41412801 12.70933969 15.95818099 43.48706704 50.86340983 26.18153328 downscale: 26.18153328 8.13172798 12.70933969 43.48706704 26.18153328 clean: 8.13172798 12.70933969 43.48706704 convolution: 10.39855066 -4.51755254 -11.63507628 14.92788394 -21.4212545 10.88151357 22.65778012 -21.29184498 10.39855066 downscale: 10.39855066 -11.63507628 -21.4212545 22.65778012 10.39855066] clean : -11.63507628 -21.4212545 22.65778012
Approximations Details

Et voilà ! nos coefficients d'approximations et de détails sont équivalents à ceux de pywt !

Pad' Patrouille

Si besoin, pywt intègre une fonction pywt.pad() permettant d'effectuer ce travail de padding automatiquement :

pywt.pad( [1, 20, 3, 40], len(wavelet_dec_lo), 'symmetric' ) array([ 40, 3, 20, 1, 1, 20, 3, 40, 40, 3, 20, 1 ])

Maintenant que nous avons vu comment utiliser l'ondelette Daubechies-2 avec pywt et numpy, effectuons nous-même nos propres caluls sans aucune librairie.

Tout d'abord, nous allons regrouper nos différents groupes de données qui vont nous servir, en incluant les paddings :

Middle
Left Padding Right Padding

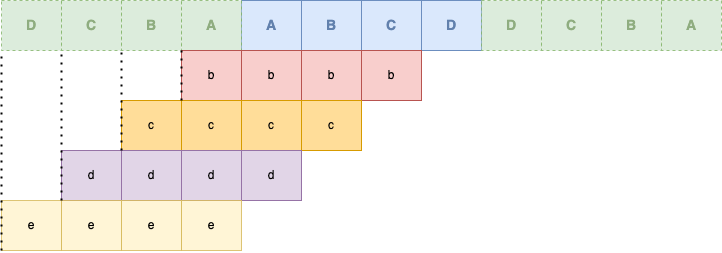
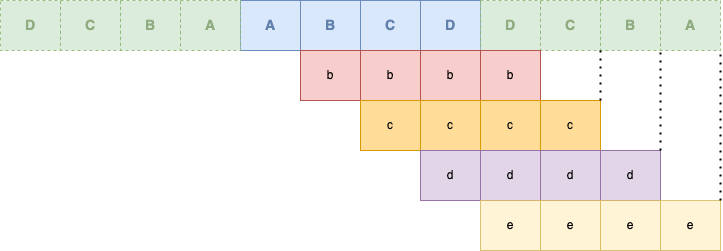
Vous voyez nos différents groupes de données avec qui nous allons appliquer nos 4 coefficients de décomposition high-pass ou low-pass.

Pour les récupérer, nous allons directement utiliser les fonctions scaling et wavelet qui vont nous donner (aussi) les coefficients pour le high-pass et low-pass : 

import pywt

# on récupère les propriétés de Db2
wavelet = pywt.Wavelet("db2")
(phi, psi, x) = wavelet.wavefun(level=1)

# Scaling function (hi->approximation) (phi) :
0.0 0.6830127018922194 1.1830127018922194 0.3169872981077807 -0.18301270189221933 0.0 0.0

# Wavelet function (lo->detail) (psi) :
0.0 -0.18301270189221933 -0.3169872981077807 1.1830127018922194 -0.6830127018922194 0.0 0.0
Quelle est la différence entre les coefficients des filtres et les valeurs données par scaling et wavelet ?

C'est la même chose, sauf que nous appliquons ou supprimons le coefficient de normalisation selon le sens :

Suppression
normalisation 		Ajout
normalisation

Un exemple avec le premier coefficient wavelet_dec_lo (-0.129..) :

-0.18301270189221933 * 1/sqrt(2) = -0.12940952255126038585

Maintenant que nous avons nos coefficients de scaling (0.68, 1.18, 0.31, -0.18), qui va nous servir pour le filtre high-pass, nous pouvons effectuer le calcul, il suffit de multiplier chaque donnée avec son coefficient attitré :

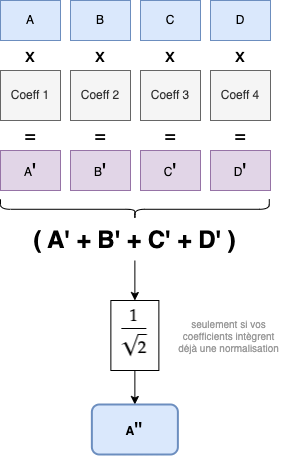
# Rappel des coefficients de filtrage :
# 0.6830127018922194 1.1830127018922194 0.3169872981077807 -0.18301270189221933

     1 *  0.6830127018922194   =   0.6830127018922194 
    20 *  1.1830127018922194   =  23.6602540378443880
     3 *  0.3169872981077807   =   0.9509618943233421
    40 * -0.18301270189221933  =  -7.32050807568877320

Puis, nous additionnions toutes les valeurs :

0.6830127018922194 + 23.6602540378443880 + 0.9509618943233421 + -7.32050807568877320 = 17.97372055837117630

Ah... nous avons pas la même valeur. Normalement, nous devrions avoir 12.70933969. Il nous manque un petit calcul, celui avec le coefficient de normalisation :

17.97372055837117630 * 1/sqrt(2) = 12.70933968997631815112

Voila notre premier coefficient d'approximation pour notre séquence initiale [1, 20, 3, 40] et maintenant, nous devons effectuer les calculs pour l'ensemble des séquences :

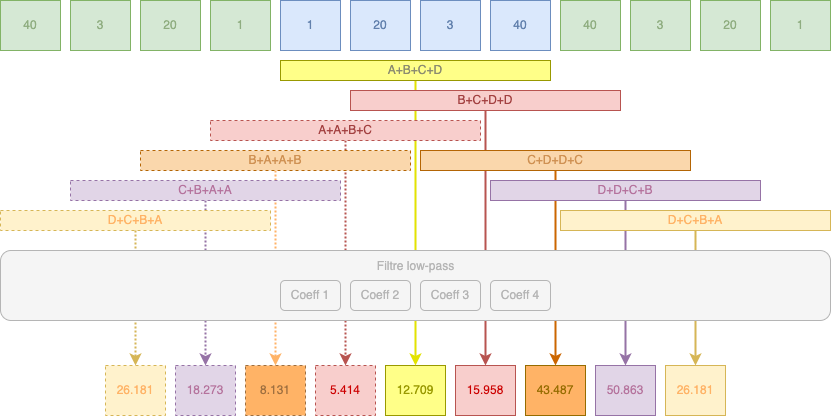
Maintenant que nous avons nos différents coefficients, nous devons procéder à un downscale. Précédemment, notre downscale était implicite, nous additionnons nos deux valeurs et appliquions une division et donc nous conservions qu'une seule valeur. Ici, avec nos coefficients, le downscale n'est pas une division, mais carrément une suppression d'une valeur des deux valeurs pour n'en conserver une seule :

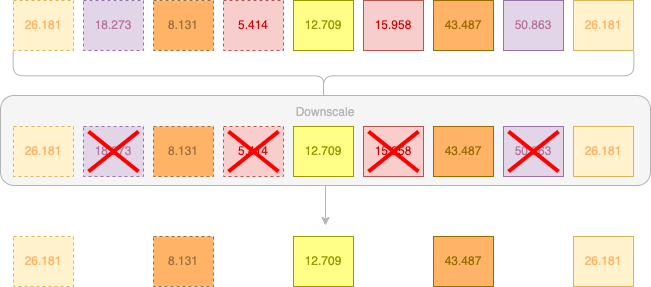
Nos valeurs intermédiaires sont donc 26.181, 8.131, 12.709, 43.487 et 26.181.

Maintenant, nous allons appliquer un cleanup, nous allons supprimer les deux valeurs de bords car elles nous sont maintenant inutiles :

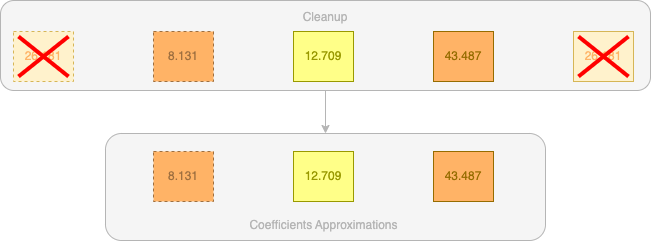
Et voila !

Nous avons notre première décomposition pour nos coefficients d'approximation. Maintenant, nous devons effectuer la même chose avec les coefficients de scaling (ou high-pass) pour les obtenir.

À la fin, vous vous retrouverez avec ces valeurs :

Approximations Details
8.13172798 12.70933969 43.48706704 -11.63507628 -21.4212545 22.65778012

Vous venez de faire votre premier calcul de décomposition avec les wavelets Daubechies-2 à l'aide des filtres passe-haut et passe-bas et leurs coefficients low-pass (scaling function) et leurs coefficients high-pass (wavelet function).

Vous retrouverez un programme utilisant ce principe à cette adresse. Le programme vous montre une décomposition Debauchies-2 avec les méthodes pywt, numpy et from-scratch.

Maintenant que nous avons vu cela, nous pouvons nous attaquer aux ondelettes utilisées dans le JPEG2000 : Daubechies 9/7 (surnommé parfois CDF 9/7) et LeGall 5/3 (surnommé parfois LGT 5/3).

Les coefficients pour le JPEG2000 (Daubechies 9/7, LeGall 5/3)

Le JPEG2000 possède plusieurs profils, ce sont des méthodes d'utilisation.

Pour un DCP, c'est le profil irréversible qui a été choisi, ce profil indique une utilisation de la compression avec pertes.

Cela veut dire que le fichier qui sortira après la compression ne pourra pas retourner à son fichier d'origine, vous aurez perdu de la matière pour les besoins de la compression ( à contrario d'une compression sans perte qui permet de retrouver le fichier d'origine, un exemple avec une compression ZIP : votre fichier est compressé mais en le décompressant, vous retrouvez le fichier d'origine).

Le JPEG2000 peut être utilisé sans pertes, c'est le profil réversible qui permettrait de retrouver le fichier d'origine. Ce choix a été fait uniquement pour le format d'échange et de préservation IMF, et non le DCP.

Le JPEG2000 utilise deux wavelets différentes : Daubechies 9/7 et LeGall 5/3 :

Les deux types de wavelets auront des coefficients différents et également des coefficients différents entre passe-bas et passe-haut.

Pour le JPEG2000 DCP, nous utiliserons Daubechies 9/7.

Avec Daubechies 9/7, nous avons des coefficients passe-haut et passe-bas avec différentes valeurs - et surtout le nombre de coefficients diffère entre les deux filtres :

Voici les coefficients Daubechies 9/7 et LeGall 5/3 :

Coefficients Daubechies 9/7
Décomposition
Position
(k)		 Lowpass filter (hk) Highpass filter (gk)
0 +0.6029490182363579 +1.115087052456994
±1 +0.2668641184428723 -0.5912717631142470
±2 -0.07822326652898785 -0.05754352622849957
±3 -0.01686411844287495 +0.09127176311424948
±4 +0.02674875741080976 0
autres
valeurs		 0 0
Recomposition
Position
(k)		 Lowpass filter (hk) Highpass filter (gk)
0 +1.115087052456994 +0.6029490182363579
±1 +0.5912717631142470 -0.2668641184428723
±2 -0.05754352622849957 -0.07822326652898785
±3 -0.09127176311424948 +0.01686411844287495
±4 0 +0.02674875741080976
autres
valeurs		 0 0
Coefficients LeGall 5/3
Décomposition
Lowpass filter (hk) Highpass filter (gk)
0 6 / 8 1
±1 2 / 8 -1 / 2
±2 -1 / 8 0
Recomposition
Lowpass filter (hk) Highpass filter (gk)
0 1 6 / 8
±1 1 / 2 -2 / 8
±2 0 -1 / 8

N'oubliez pas que ces coefficients ne sont que les résultats de longues équations. Pour nos besoins, nous n'en avons pas forcément besoin car ce dont nous avons besoin c'est d'un calcul rapide. Vous retrouverez les équations derrière ces coefficients dans de nombreuses publications sur les wavelets.

Tout de suite, vous vous dites que vous ne voyez que 5 coefficients et 4 coefficients dans le tableau Daubechies 9/7, alors pourquoi parler de 9/7 ?

Dans la plupart des tableaux, vous verrez une colonne (souvent nommée "k") avec des symboles ±, c'est simplement que la valeur du centre est celle avec k0 et le reste sont des valeurs se trouvant à droite et à gauche de ce centre. Un peu comme un effet miroir dont le centre est k0.

Ainsi, si nous prenons notre tableau, voici notre matrice complète de coefficients (réduites à 3 chiffres après la virgule) :

Position /
Filtre		 > -4 -3 -2 -1 0 +1 +2 +3 +4 <
Low-pass 0 +0.026 -0.016 -0.078 +0.266 +0.602 +0.266 -0.078 -0.016 +0.026 0
High-pass 0 +0.000 +0.091 -0.057 -0.591 +1.115 -0.591 -0.057 +0.091 +0.000 0
middle

Pywt n'intègre pas (encore) Daubechies 9/7. Pour l'intégrer par nous-même, il suffit d'intégrer nos 4 matrices de coefficients dans une nouvelle classe Wavelet :

# Nos coefficients Daubechies 9/7
dec_low  = [0.0, 0.026748757411,  -0.016864118443, -0.078223266529,  0.266864118443, 0.602949018236,  0.266864118443, -0.078223266529, -0.016864118443, 0.026748757411]
#                                                                                    ┗━━ middle ━━┛
dec_high = [0.0, 0.091271763114,  -0.057543526229, -0.591271763114,  1.11508705,    -0.591271763114, -0.057543526229,  0.091271763114,             0.0,            0.0]
#                                                                    ┗━middle━┛
rec_low  = [0.0, -0.091271763114, -0.057543526229,  0.591271763114,  1.11508705,     0.591271763114, -0.057543526229, -0.091271763114,             0.0,            0.0]
#                                                                    ┗━middle━┛
rec_high = [0.0, 0.026748757411,   0.016864118443, -0.078223266529, -0.266864118443, 0.602949018236, -0.266864118443, -0.078223266529,  0.016864118443, 0.026748757411]
#                                                                                    ┗━━ middle ━━┛

wavelet = pywt.Wavelet(
    name='Daubechies CDF 9/7',
    filter_bank=(dec_low, dec_high, rec_low, rec_high)
)
wavelet.orthogonal = False
wavelet.biorthogonal = True

print(wavelet)
Wavelet Daubechies CDF 9/7
  Family name:
  Short name:
  Filters length: 10
  Orthogonal:     False
  Biorthogonal:   True
  Symmetry:       unknown
  DWT:            True
  CWT:            False

print(*wavelet.dec_lo)
 0.0             0.026748757411
-0.016864118443 -0.078223266529
 0.266864118443  0.602949018236
 0.266864118443 -0.078223266529
-0.016864118443  0.026748757411

print(*wavelet.dec_hi)
 0.0             0.091271763114
-0.057543526229 -0.591271763114
 1.11508705     -0.591271763114
-0.057543526229  0.091271763114
 0.0             0.0

# Récupération des fonctions scaling et wavelet  
(phi_decomp, psi_decomp, phi_recomp, psi_recomp, x) = wavelet.wavefun(level=1)

print(*phi_decomp)
 0.0                  0.03782845550726404 -0.023849465019556843
-0.11062440441843718  0.37740285561283066  0.8526986790088938
0.37740285561283066  -0.11062440441843718 -0.023849465019556843
 0.03782845550726404  0.0                  0.0
 0.0                  0.0                  0.0
 0.0                  0.0                  0.0

print(*psi_decomp)
 0.0                0.0                 0.0 
-0.1290777652575232 0.08137883521982373 0.8361845464440707
-1.5769712293366058 0.8361845464440707  0.08137883521982373
-0.1290777652575232 0.0                 0.0
 0.0                0.0                 0.0
 0.0                0.0                 0.0

Avec cela, nous pouvons utiliser pywt pour calculer nos coefficients:

signal = [ 1, 2, 3, 4 ] print( *pywt.dwt( signal, wavelet ) ) [ 3.89163373 1.94154601 1.10836627 3.05845399 3.89163373 1.94154601] => Approximation [-0.12500001 -0.30754353 0.125 0.30754352 -0.12500001 -0.30754353] => Detail

Vous retrouverez dans ce programme avec un calcul approximations et détails avec pywt

Et nous pouvons appliquer cette méthode avec numpy également :

import numpy as np

signal = [1, 2, 3, 4]
wavelet_dec_low = [
     0.0,
     0.026748757411,
    -0.016864118443,
    -0.078223266529,
     0.266864118443,
     0.602949018236,
     0.266864118443,
    -0.078223266529,
    -0.016864118443,
     0.026748757411
]

signal_padded = pywt.pad(signal, len(wavelet_dec_low), 'symmetric')

print(signal_padded)
[2 1 1 2 3 4 4 3 2 1 1 2 3 4 4 3 2 1 1 2 3 4 4 3]

# convolution + downscale + cleanup
approximation = np.convolve(signal_padded, wavelet_dec_low, 'valid')[::2][1:-1]
# convolution = 3.0584539885929996 3.891633728893 3.8916337288930007 3.058453988593 1.9415460114070002 1.1083662711070001 1.1083662711070001 1.9415460114069998 3.0584539885929996 3.891633728893 3.8916337288930007 3.058453988593 1.9415460114070002 1.1083662711070001 1.1083662711070001
# downscale   = 3.0584539885929996 3.8916337288930007 1.9415460114070002 1.1083662711070001 3.0584539885929996 3.8916337288930007 1.9415460114070002 1.1083662711070001

# final result
print(*approximation)
3.8916337288930007 1.9415460114070002
1.1083662711070001 3.0584539885929996
3.8916337288930007 1.9415460114070002

Il suffit de faire la même chose pour les coefficients de détails avec wavelet_dec_high.

wavelet_dec_high = [
     0.0,
     0.091271763114,
    -0.057543526229,
    -0.591271763114,
     1.11508705,
    -0.591271763114,
    -0.057543526229,
     0.091271763114,
     0.0,
     0.0
]

# convolution + downscale + cleanup
detail = np.convolve(signal_padded, wavelet_dec_high, 'valid')[::2][1:-1]
# convolution = 0.3075435163990001 0.3075435163990001 -0.12500000737299982 0.12499999508300005 -0.30754352868899987 -0.30754352868899976 0.12499999508300014 -0.12500000737299938 0.3075435163990001 0.3075435163990001 -0.12500000737299982 0.12499999508300005 -0.30754352868899987 -0.30754352868899976 0.12499999508300014
# downscale   = 0.3075435163990001 -0.12500000737299982 -0.30754352868899987 0.12499999508300014 0.3075435163990001 -0.12500000737299982 -0.30754352868899987 0.12499999508300014

# final result
print(*detail)
-0.12500000737299982 -0.30754352868899987
 0.12499999508300014  0.3075435163990001
-0.12500000737299982 -0.30754352868899987

Retrouvez la méthode numpy dans ce programme.

Voyons maintenant notre propre méthode de calcul en commençant par la sortie :

1. Approximation : 3.0584539885929996 2. Approximation : 3.891633728893 3. Approximation : 3.8916337288930007 4. Approximation : 3.058453988593 5. Approximation : 1.9415460114070002 6. Approximation : 1.1083662711070001 7. Approximation : 1.1083662711070001 8. Approximation : 1.9415460114069998 9. Approximation : 3.0584539885929996 10. Approximation : 3.891633728893 11. Approximation : 3.8916337288930007 12. Approximation : 3.058453988593 13. Approximation : 1.9415460114070002 14. Approximation : 1.1083662711070001 15. Approximation : 1.1083662711070001

Notre k0 sera appliqué sur la première donnée :

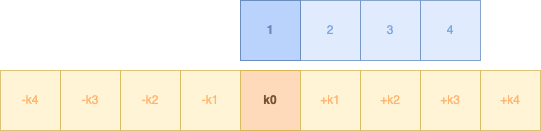
On voit tout de suite le souci : nous n'avons pas assez de donnée à droite comme à gauche. Pour cela, nous appliquons notre méthode de padding (mode symétrie) :

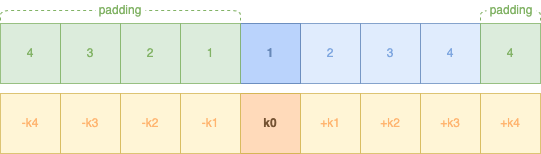
Bien entendu, nous devons appliquer sur l'ensemble de nos 4 données :

A partir de là, nous n'avons pas terminé, si vous remarquez, nous avons encore 4 coefficients en arrière (-k1, -k2, -k3 et -k4). Nous devons arriver à faire passer tous nos coefficients jusqu'à la dernière donnée, donc jusqu'à ce que -k4 puisse côtoyer la donnée 4 :

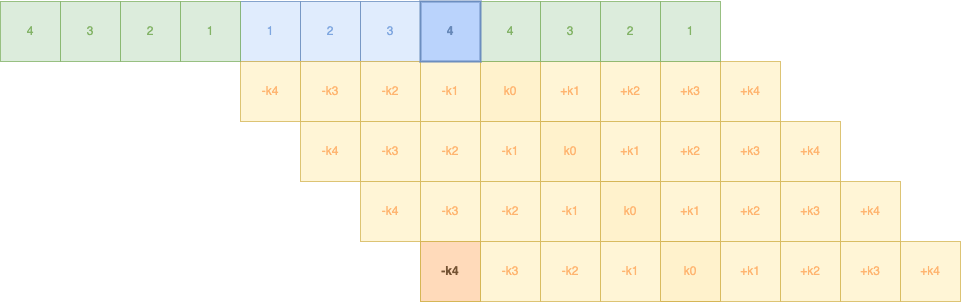
Et nous effectuons la même chose de l'autre côté.

Un petit détail, nous n'avons pas que 9 coefficients mais 10, le 0.0 supplémentaire, nous aurons donc un -k5, ainsi voici la matrice complète de décalage et de calculs entre coefficients et données :

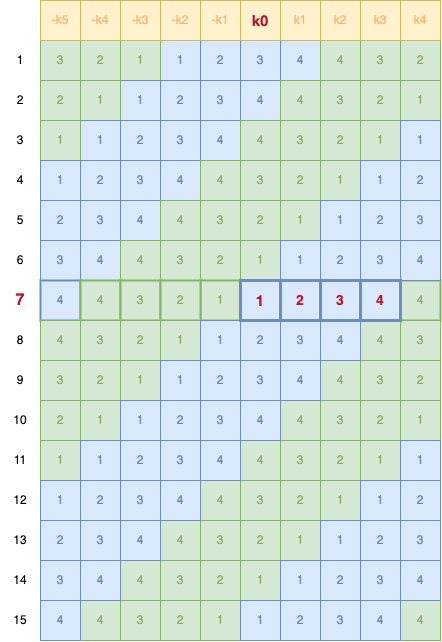
Pour les calculs, ils sont relativement simples et nous les avons déjà vus :

wavelet_dec_low  = [
     0.0,                  # -k5   (notre ajout pour avoir 10 coefficients)
     0.026748757411,       # -k4
    -0.016864118443,       # -k3
    -0.078223266529,       # -k2
     0.266864118443,       # -k1
     0.602949018236,       #  k0
     0.266864118443,       # +k1
    -0.078223266529,       # +k2
    -0.016864118443,       # +k3
     0.026748757411        # +k4
]

a = signal[0] * wavelet_dec_low[0]
b = signal[1] * wavelet_dec_low[1]
c = signal[2] * wavelet_dec_low[2]
d = signal[3] * wavelet_dec_low[3]
e = signal[4] * wavelet_dec_low[4]
f = signal[5] * wavelet_dec_low[5]
g = signal[6] * wavelet_dec_low[6]
h = signal[7] * wavelet_dec_low[7]
i = signal[8] * wavelet_dec_low[8]
j = signal[9] * wavelet_dec_low[9]

print("Approximation :", (a+b+c+d+e+f+g+h+i+j))

Maintenant, prenons notre signal décalé de la ligne 7 (4, 4, 3, 2, 1, 1, 2, 3, 4, 4) et appliquons nos coefficients low-pass :

#   S *  LowPass
a = 4 *  0.0
b = 4 *  0.026748757411
c = 3 * -0.016864118443
d = 2 * -0.078223266529
e = 1 *  0.266864118443
f = 1 *  0.602949018236
g = 2 *  0.266864118443
h = 3 * -0.078223266529
i = 4 * -0.016864118443
j = 4 *  0.026748757411

Approximation = (a+b+c+d+e+f+g+h+i+j) 
Approximation = 1.1083662711070001

Si nous comparons avec notre tableau :

1. Approximation : 3.0584539885929996 2. Approximation : 3.891633728893 3. Approximation : 3.8916337288930007 4. Approximation : 3.058453988593 5. Approximation : 1.9415460114070002 6. Approximation : 1.1083662711070001 7. Approximation : 1.1083662711070001 8. Approximation : 1.9415460114069998 9. Approximation : 3.0584539885929996 10. Approximation : 3.891633728893 11. Approximation : 3.8916337288930007 12. Approximation : 3.058453988593 13. Approximation : 1.9415460114070002 14. Approximation : 1.1083662711070001 15. Approximation : 1.1083662711070001

Et pour les coefficients de détails, c'est pareil avec les coefficients high-pass. Notez que nous n'avons pas eu besoin de jouer avec la racine-carré-de-2, les coefficients intègrent déjà ~~tout le bordel~~ tous les calculs sur la normalisation.

Vous retrouverez l'ensemble des calculs bruts dans ce programme.

Et la méthode Lifting ?

Précédemment, nous avons vu comment effectuer des calculs wavelets via le principe de la convolution. Cependant, il existe une autre méthode, la méthode lifting 1, 2.

Elle diffère par la méthode de calcul, des différentes étapes et surtout des coefficients finaux (mais pas des équations de convolutions à l'origine qui seront retravaillées pour être "traduit" pour devenir la méthode lifting).

La méthode lifting a été développée afin d'accélérer les calculs lors d'une décomposition. Elles ont été développées par Wim Sweldens et Ingrid Daubechies, dès 1996.

Au lieu d'un ensemble de filtres de coefficients (bank filters), la méthode lifting utilisent des étapes de predicts (prédiction) et d'update : un simple mécanisme de prévision et de mise-à-jour est utilisé dont voici un schéma simplifié 5 :

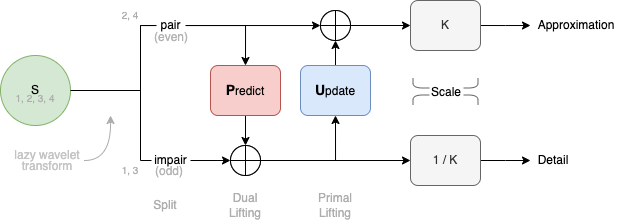
Cela est accompagné d'un downscale placé en amont des calculs plutôt qu'en aval. Autrement dit, nous effectuons un downscale avant nos filtrages Predict/Update. Cela a un intérêt direct: nos calculs ne s'appliquent plus que sur la moitié des données.

La méthode lifting a aussi un intérêt très concret: Étant plus simple, cette méthode consomme moins de ressources. On parle d'une amélioration allant jusqu'à 80%.

Avec le passage via predicts et update, nos coefficients sont eux aussi moins nombreux, nous passons de 9+7 à seulement 5 coefficients de filtrage. Avec la convolution, nous avons 9 multiplications et 14 additions. Avec la méthode lifting, nous passons à 6 multplications et 8 additions.

L'autre avantage est que l'on peut transformer les différentes ondelettes à filter-banks en version liftée. Ainsi, notre Daubechies 9/7 a été traduit de la sorte pour correspondre à la méthode liftée :

Etape Coefficient
Predict 1 -1.586134342059924
Update 1 -0.052980118572961
Predict 2 0.882911075530934
Update 2 0.443506852043971
Scale 6 1.1496043988602418

Vous remarquez qu'il existe deux étapes Predicts et Updates, pour Daubechies, elles seront à la suite juste avant le scale final :

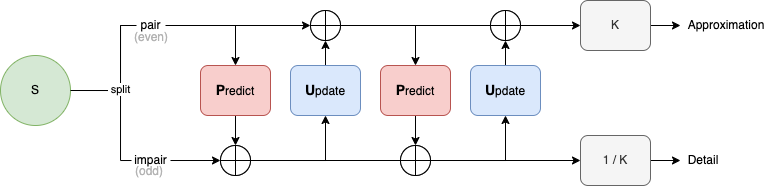
Ce qui donne avec les différentes valeurs :

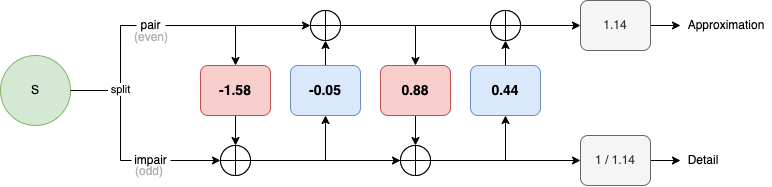
Pour les équations :

  d = odd - P(even)
  c = even + U(d) 
  
  P étant l'opérateur de Prediction (Dual lifting)
  U étant l'opérateur d'Update (Primal lifting)

A compléter

Fast Wavelet Transform

La méthode Fast Wavelet Transform est la dernière méthode choisie pour les nouveaux DCP SMPTE JPEG2000. Cette méthode permet d'accelérer la compression et la décompresson mutiscale. A l'heure actuelle, la quasi-majorité des décodeurs DCP permettent de lire cette nouvelle méthode, seules quelques très vieux décodeurs DCP peuvent avoir du mal (on parle de quelques flashs lumineux lors de lectures).

Compléter ce paragraphe pour parler un peu plus de la méthode FWT

High Throughput JPEG 2000 (HTJ2K)

Le HTJ2K est une évolution de l'encodage JPEG2000 qui permet d'améliorer ces performances. Le HTJ2K s'attaque essentiellement à la partie arithmétique du block coder. Pour l'instant, cette méthode est surtout orientée pour l'IMF, mais il est prévu que cette évolution arrive aussi pour la projection donc dans les DCP.

Compléter ce paragraphe pour parler un peu plus de la méthode HTJ2K via white-paper : https://www.htj2k.com/wp-content/uploads/white-paper.pdf

Le JPEG2000 normé pour le cinéma numérique

Le JPEG2000 dans un DCP est normé par ces différentes publications :

Voici les principaux critères du JPEG2000 utilisé dans le cinéma numérique :

D-Cinema IMF
Pertes Avec pertes Sans pertes
Bitdepth 12 bits
12 bits par composant
12 x 3 = 36 bits par pixel		 12 ou 16 bits
Espace Colorimétrique
(Colorspace)		 YCbCr 7
(Input: X'Y'Z')		 YUV
Subsample Non
Seulement 4:4:4		 Non
Seulement 4:4:4
Transformation colorimétrique ICT
(Irreversible Color Transformation)		 RCT
(Reversible Color Transformation)
Transformation Wavelet CDF 9/7
Irreversible avec filtres 9/7
Précision minimum: 16 bits fixed point		 LeGall 5/3
Réversible avec filtres 5/3
Précision minimum: 16 bits fixed point
Quantification Oui Non
Rate Control Oui Non
Progression Order CPRL
(Component Position Resolution Layer)

Les résolutions valides sont 2048x1080 (2K) et 4096x2160 (4K). Notez que vous aurez des résolutions inférieures de par le principe du JPEG2000 multi-résolutions :

2K 4K
2048 x 1080 4096 x 2160
1024 x 540 2048 x 1080
512 x 270 1024 x 540
256 x 135 512 x 270
128 x 68 256 x 135
128 × 68

Il existera donc 6 résolutions, dont 5 décompositions (appelées aussi Wavelet Transformations Levels).
Voir paragraphe Resolutions et Decompositions pour de plus amples informations.

L'image et (l'unique) tile sont collés au bord (0, 0) (donc les positions de décalage XOsiz & YOsiz et les positions de décalage XTOsiz & YTOsiz seront toujours à 0)

La fonctionnalité Region Of Interest (ROI) n'est pas acceptée.

Workflow du JPEG2000

La transformation en JPEG2000 s'effectue par différentes étapes dans cet ordre :

La version complète du workflow JPEG2000 :

Preprocessing Core Processing Bit-Stream
Tiling Discrete Wavelet Transformation Precincts
DC-Level Shifting Quantization Code-blocks
Component Transformation Entropy Coding Layers
Packets

Voyons les différentes principales étapes :

Tiling

La norme JPEG2000 permet de créer des découpages de l'image qu'on appelle "tiles". Les tiles sont des subdivisions de l'image avant les étapes de transformation colorimétrique et de transformation wavelet. Cela est utile si on travaille sur des systèmes avec peu de ressources (CPU/Ram).

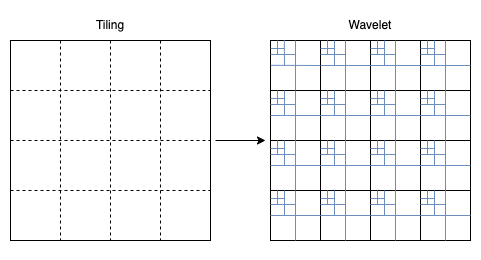
Dans notre cas du JPEG2000 cinéma, cela n'est pas utile, le processus de wavelet effectuera son travail sur l'entièreté de l'image, l'image n'a qu'une seule Tile :

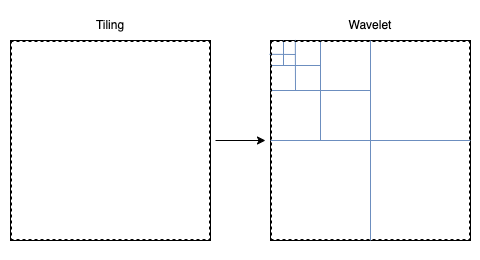
Il existe cependant une petite subtilité si nous prenons les spécifications DCI :

Each compressed frame of a 2K distribution shall have exactly 3 tile parts. Each tile part shall contain all data from one color component. Each compressed frame of a 4K distribution shall have exactly 6 tile parts. Each of the first 3 tile parts shall contain all data necessary to decompress one 2K color component.

Nous aurons donc 3 tiles pour le 2K, et 6 tiles pour le 4K (3 pour le 2K, 3 pour le 4K). Mais d'où proviennent ces tiles ? Ce ne sont pas des tiles découpant l'image mais découpant les composantes (RGB ou X'Y'Z'). Chaque composante va passer séparément dans les différentes étapes de transformations :

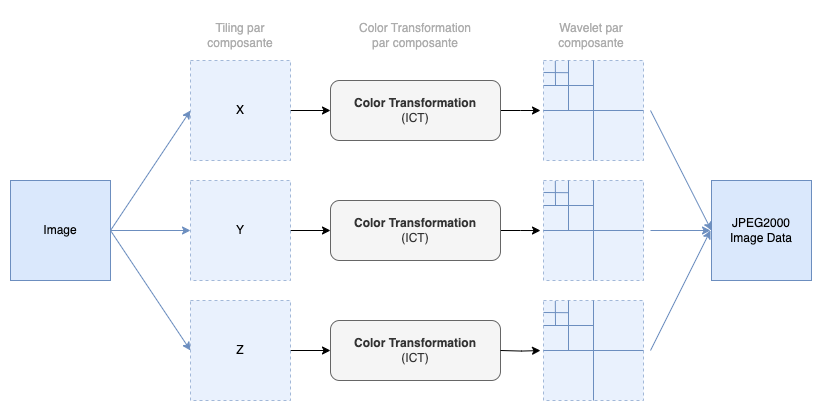
En analysant deux JPEG2000, nous pouvons voir les différents tiles spécifiques au D-Cinema :

# Image 2K avec ses 3 tiles
$ jpeg2000-parser.py "black_2k.j2c" | grep "Start of tile-part"
[SOT] Start of tile-part      ⬅ Tile 1   -   Component A - 2K
[SOT] Start of tile-part      ⬅ Tile 2   -   Component B - 2K
[SOT] Start of tile-part      ⬅ Tile 3   -   Component C - 2K
  
# Image 4K avec ses 6 tiles
$ jpeg2000-parser.py "black_4k.j2c" | grep "Start of tile-part"
[SOT] Start of tile-part      ⬅ Tile 1   -   Component A - 2K
[SOT] Start of tile-part      ⬅ Tile 2   -   Component B - 2K
[SOT] Start of tile-part      ⬅ Tile 3   -   Component C - 2K
[SOT] Start of tile-part      ⬅ Tile 4   -   Component A - 4K
[SOT] Start of tile-part      ⬅ Tile 5   -   Component B - 4K
[SOT] Start of tile-part      ⬅ Tile 6   -   Component C - 4K

Transformation colorimétrique

Selon le procédé (ICT ou RCT), une conversion colorimétrique est opérée soit en YCbCr (luminance + chrominance bleue + chrominance rouge), soit en YUV :

À titre indicatif, voici les différentes équations et calculs à opérer dans les cas ICT & RCT :

Je vous invite chaudement à lire la note [8] si vous voulez en savoir plus à propos du X'Y'Z' avec ICT.

Subbands

Nous générons l'ensemble des subbands (LL, HL, LH, HH) que nous avons vu précédemment : ce sont nos coefficients d'approximations et de details.

Voici l'ordre de priorisation des subbands (LL, HL, LH, HH) lors d'une recomposition :

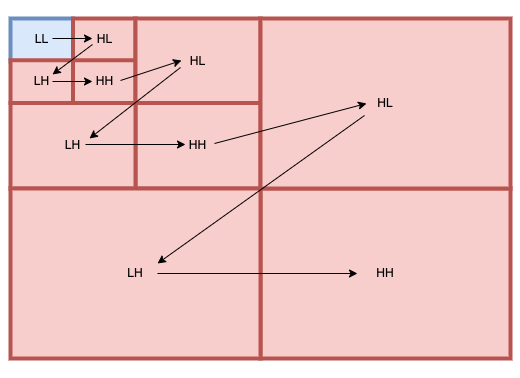
Pour décompresser les différentes résolutions, nous commençons par lire notre tout premier LL qui contient nos différents coefficients d'approximations (notre énergie de base). De là, nous allons compléter notre première résolution (toujours basse), en utilisant les coefficients de détails HL, puis LH et enfin HH. Nous arrivons à un niveau de décomposition, nous avons un nouveau LL. A partir de là, nous pouvons continuer dans le même ordre pour arriver à notre toute dernière résolution, la plus haute disponible.

Quantization

Nous allons quantifier (quantization) les données. Cela veut dire qu'on va réduire leur précision. Cette étape est destructrice, donc elle ne sera utilisée que pour le JPEG2000 CDF 9/7 pour le D-Cinema.

Codeblocks & Precincts

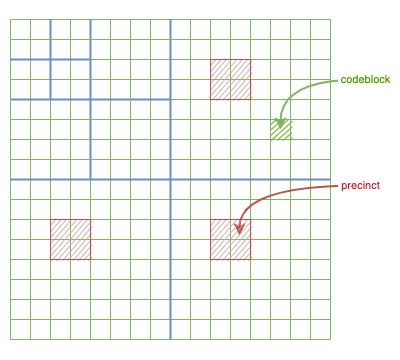
On va découper en petits blocs appelées codeblocks et regrouper les codeblocks par groupes appelées precints 9 :

Les tailles des codeblocks sont fixées à 32 x 32 pixels. 

$ jpeg2000-parser.py "black_4k.j2c" | grep "CodeBlockSize"
COD - CodeBlockSize : 32 x 32

Le codeblock est la plus petite structure géométrique d'un JPEG2000.

Les tailles des precincts sont fixées à 256x256 pixels.
(à l'exception dans la dernière subband où les precincts seront d'une taille de 128x128. 

# Image 4K (7 résolutions) : 
$ jpeg2000-parser.py "black_4k.j2c" | grep "PrecinctSize"
COD - PrecinctSize 1 : 128 x 128
COD - PrecinctSize 2 : 256 x 256
COD - PrecinctSize 3 : 256 x 256
COD - PrecinctSize 4 : 256 x 256
COD - PrecinctSize 5 : 256 x 256
COD - PrecinctSize 6 : 256 x 256
COD - PrecinctSize 7 : 256 x 256

Les precincts sont des regroupements de codeblocks.

Les precincts sont utilisés pour permettre une spécialisation d'une zone : les precincts sont des zones de l'image en commun entre les différentes subbands. Chaque precincts de chaque subbands sont liés entre elles et elles décrivent une partie de votre image. Si vous voulez reconstituer une zone particulière, il suffit de lire le precinct précis venant du HL, le precinct précis venant du HL et enfin le precinct précis venant du HH.

A titre informatif, le regroupement des 3 precincts d'une résolution spécifique est appelée Packet. Dans un paquet, vous aurez la suite des codeblocks des 3 precincts, l'un à la suite de l'autre; Voici un exemple de packet avec des precincts d'une taille de seulement de 4 codeblocks :

#    ╭┄┄┄ Precinct 1 ┄┄┄╮╭┄┄┄ Precinct 2 ┄┄┄╮╭┄┄┄ Precinct 3 ┄┄┄╮
    ┏━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┳━━━━┓
    ┃ HL ┊ HL ┊ HL ┊ HL ┃ LH ┊ LH ┊ LH ┊ LH ┃ HH ┊ HH ┊ HH ┊ HH ┃
    ┗━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┻━━━━┛   
#   ╰┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ Packet ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄╯

Resolutions et Decompositions

Le nombre de résolution dans un JPEG2000 est dépendant du nombre de décomposition.

Pour savoir combien vous avez de résolution, il suffit de connaître le nombre de décomposition et de l'augmenter d'un 10 :

Resolution    = ( Decomposition + 1 )
Decomposition = ( Resolution    - 1 )

Notez que, selon les implémentations, le nombre de décompositions est également surnommé Wavelet Transform Levels ou parfois réduit en Decomp ou Dec.

Voici un tableau récapitulatif par résolution :

Nombre de résolutions

 Nombre de Décompositions
(Wavelet Transform Level)
Résolution 2K 6 5
Résolution 4K 7 6

Analyse des différents niveaux de décomposition sur deux images 2K et 4K : 

$ jpeg2000-parser.py "black_2k.j2c" | grep "Decomposition levels"
COD - Decomposition levels : 5

$ jpeg2000-parser.py "black_4k.j2c" | grep "Decomposition levels"
COD - Decomposition levels : 6

Voici les différentes résolutions que nous avons déjà vu précédemment :

Decomposition
Level		 2K 4K
1 2048 x 1080 4096 x 2160
2 1024 x 540 2048 x 1080
3 512 x 270 1024 x 540
4 256 x 135 512 x 270
5 128 x 68 256 x 135
6 128 × 68

A l'intérieur du JPEG200 D-Cinema

Le fichier JPEG2000 est construit un peu comme un MXF, vous aurez différents blocs de métadonnées comprenant nos blocs de données.

Pour la suite de ce paragraphe, nous utiliserons l'image black_4k.j2c :

Un simple... écran noir, rien de plus simple ;-)

Regardons l'intérieur d'un fichier en visualisant ces données brutes à l'aide d'un éditeur hexadécimal :

Le fichier 2K :

Le fichier 4K :

Nous allons maintenant analyser les données brutes du fichier 4K.

Un fichier JPEG2000 démarre toujours par un code appelé Start of Codestream avec une valeur de 0xFF4F et se termine par un code appelé End of Codestream avec une valeur de 0xFFD9 :

Ces deux markers - de 2 octets chacun - représentent un marqueur de début et de fin de fichier.

Après ce premier marker Start of Codestream, vous aurez une suite de markers à différents endroits de votre JPEG2000, chaque marker est le début d'un bloc de métadonnées :

Les 2 octets (16 bits) qui suivent nos différents markers sont les tailles, suivi des données du bloc :

(oubliez pour l'instant les markers FF93, ils sont particuliers...)

Pour notre premier bloc de métadonnées, nous avons une valeur pour la taille de 0x002F correspondant au chiffre 47 en décimal : nos données seront donc de 47 octets. Nous devons cependant retrancher les 2 octets provenant de la taille de .. la taille. La véritable taille des données est donc de 45 octets :

Si nous résumons : nous avons un identifiant (marker), une taille et des données. Cela ne vous rappelle rien ? Si vous avez lu le chapitre KLV, vous aurez déjà identifié la structure type d'un KLV 11 !

Les différents KLV de métadonnées

Si vous n'avez pas lu le chapitre KLV (Key-Length-Value), voici un bref résumé :

Chaque bloc de métadonnées possède un identifiant (marker), une taille et bien évidemment des données (à l'exception d'un marker appelé Start of data, il en fallait bien un...) :

Voici les différents markers avec leurs codes et leurs descriptions :

Code Nom Identifiant JPEG2000 DCP
Delimiting Marker Segments
SOC Start of codestream 0xFF4F Oui
SOT Start of tile-part 0xFF90 Oui
SOD Start of data 0xFF93 Oui
EOC End of codestream 0xFFD9 Oui
Fixed Information Marker Segments
SIZ Image and tile size 0xFF51 Oui
Functional Marker Segments
COD Coding style default 0xFF52 Oui
COC Coding style component 0xFF53 Oui
RGN Region-of-interest 0xFF5E Interdit
QCD Quantization default 0xFF5C Oui
QCC Quantization component 0xFF5D Oui
POC Progression Order Change 0xFF5F Seulement en 4K
Pointer Marker Segments
TLM Tile-part lengths, main header 0xFF55 Oui (Requis)
PLM Packet length, main header 0xFF57 Non
PLT Packet length, tile-part header 0xFF58 Non
PPM Packed packet headers, main header 0xFF60 Interdit
PPT Packed packet headers, tile-part header 0xFF61 Interdit
Bitstream Marker Segments
SOP Start of packet 0xFF91 Non 12
EPH End of packet header 0xFF92 Non 13
Informational Marker Segments
CME Comment and extension 0xFF64 Oui (optionnel)
CRG Component registration 0xFF63 Non

En grande majorité, dans un JPEG2000 DCI, vous aurez des markers SOC, SOT, SOD, EOC, SIZ, COD, QCD, POC, TLM et CME.

Visuellement, un JPEG2000 ressemble à cela :

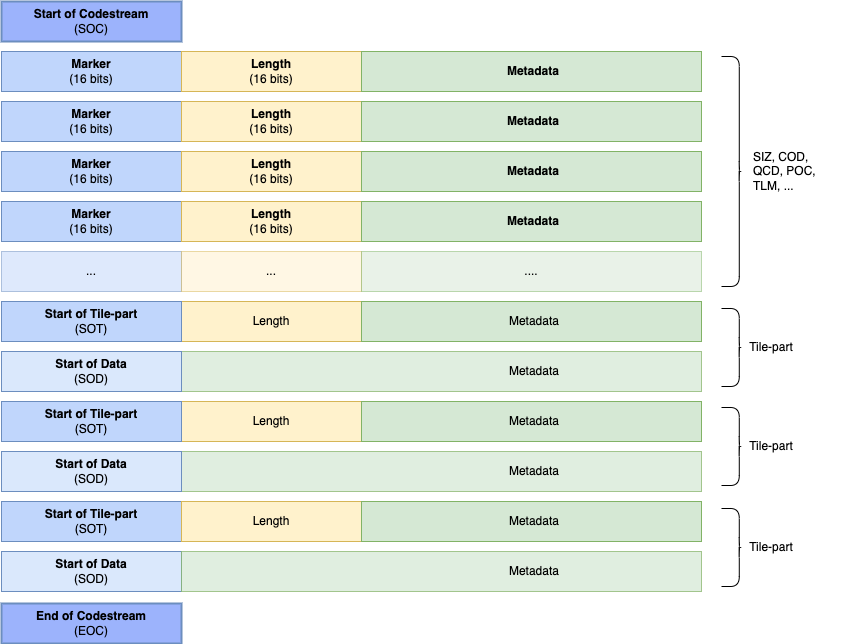
Nous constatons également que nous avons un mouton noir, notre Start of Data (SOD) qui ne respecte pas la structure d'un KLV :-)

Si nous prenons le fichier black_4k.j2c et nous le passons à notre analyseur :

# jpeg2000-parser.py "assets/JPEG2000/analyse/black_4k.j2c"
[SOC] Start of codestream                     (FF4F)
[SIZ] Image and tile size                     (FF51)
[COD] Coding style default                    (FF52)
[QCD] Quantization default                    (FF5C)
[CME] Comment and extension                   (FF64)
[POC] Progression Order Change                (FF5F)
[TLM] Tile-part lengths, main header          (FF55)
[SOT] Start of tile-part                      (FF90)
[SOD] Start of data                           (FF93)
[SOT] Start of tile-part                      (FF90)
[SOD] Start of data                           (FF93)
[SOT] Start of tile-part                      (FF90)
[SOD] Start of data                           (FF93)
[SOT] Start of tile-part                      (FF90)
[SOD] Start of data                           (FF93)
[SOT] Start of tile-part                      (FF90)
[SOD] Start of data                           (FF93)
[SOT] Start of tile-part                      (FF90)
[SOD] Start of data                           (FF93)
[EOC] End of codestream                       (FFD9)

Nous voyons nos différents blocs de métadonnées, avec leurs noms de code, leurs descriptions et leurs markers.

Étudions maintenant chacun de ces blocs plus dans le détail et leurs utilités.

N'oubliez pas que ce chapitre est orienté DCI/SMPTE. Le JPEG2000 possède des capacités, des extensions et des métadonnées plus ou moins extensibles, cette documentation montrera donc que les parties et paramètres DCI/SMPTE.

SOC : Start of codestream (FF4F)

Un fichier JPEG2000 débute par le code 0xFF4F. Rien de plus.
Vous pouvez passer ces 16 premiers bits et aller directement à votre second marker :)

SIZ : Image and tile size (FF51)

Les données sont structurées de la sorte :

Ce bloc intègre les informations sur les tailles de l'image, les nombres de composantes et des informations internes aux composantes. 

[SIZ] Image and tile size (0xff51)
size: 45 bytes
data: 45 bytes readed: 000400001000000006b4000000000000000000001000000006b4000000000000000000030b01010b01010b0101
---- Provides information about the uncompressed image such as the width and height of the reference grid,
---- the width and height of the tiles, the number of components, component bit depth,
---- and the separation of component samples with respect to the reference grid
SIZ - Rsiz   : Profile 4
SIZ - Xsiz   : 4096 px
SIZ - Ysiz   : 1716 px
SIZ - XOsiz  : 0 px
SIZ - YOsiz  : 0 px
SIZ - XTsiz  : 4096 px
SIZ - YTsiz  : 1716 px
SIZ - XTOsiz : 0 px
SIZ - YTOsiz : 0 px
SIZ - Csiz   : 3 components
SIZ - Component 1 - ssizDepth : 11 ─➤ 12 bits           Components Parameters (00001011)
SIZ - Component 1 - xRsiz     : 1 bit(s)                Horizontal separation of a sample
SIZ - Component 1 - yRsiz     : 1 bit(s)                Vertical separation of a sample
SIZ - Component 2 - ssizDepth : 11 ─➤ 12 bits           Components Parameters (00001011)
SIZ - Component 2 - xRsiz     : 1 bit(s)                Horizontal separation of a sample
SIZ - Component 2 - yRsiz     : 1 bit(s)                Vertical separation of a sample
SIZ - Component 3 - ssizDepth : 11 ─➤ 12 bits           Components Parameters (00001011)
SIZ - Component 3 - xRsiz     : 1 bit(s)                Horizontal separation of a sample
SIZ - Component 3 - yRsiz     : 1 bit(s)                Vertical separation of a sample

Une description des différentes métadonnées :

La structure des données se décompose ainsi :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF51 Notre fameux marker
Taille 16 bits uint 0-65535 Taille - 2 octets = Taille réelle des données.
Rsiz 16 bits uint 0x03 (2K)
0x04 (4K)		 Code précisant le profile du JPEG2000
Xsiz 32 bits uint 1 à 232 - 1 Taille de l'image
Ysiz 32 bits uint 1 à 232 - 1 Taille de l'image
XOsiz 32 bits uint 0 Décalage dans l'image
YOsiz 32 bits uint 0 Décalage dans l'image
XTsiz 32 bits uint 1 à 232 - 1 Taille de la tile principale
YTsiz 32 bits uint 1 à 232 - 1 Taille de la tile principale
XTOsiz 32 bits uint 0 Décalage dans la tile principale
YTOsiz 32 bits uint 0 Décalage dans la tile principale
Csiz 16 bits uint 0x03 Nombre de composant
ssiz (1) 8 bits bin 00001011 => 1 Signé ou non (bit0) et Bitdepth (bit1-7)
xRsiz (1) 8 bits uint 1 Séparation entre composante
yRsiz (1) 8 bits uint 1 Séparation entre composante
ssiz (2) 8 bits bin 00001011 => 1 Signé ou non (bit0) et Bitdepth (bit1-7)
xRsiz (2) 8 bits uint 1 Séparation entre composante
yRsiz (2) 8 bits uint 1 Séparation entre composante
ssiz (3) 8 bits bin 00001011 => 1 Signé ou non (bit0) et Bitdepth (bit1-7)
xRsiz (3) 8 bits uint 1 Séparation entre composante
yRsiz (3) 8 bits uint 1 Séparation entre composante

COD : Coding style default (FF52)

Les données sont structurées de la sorte :

Ce bloc intègre les informations de base concernant l'encodage, la décomposition, les layers, les tailles des codeblocks et des precincts :

Voici une sortie du parseur sur le bloc COD :

[COD] Coding style default (0xff52)
size: 17 bytes
data: 17 bytes readed: 0104000101060303000077888888888888
---- Describes the coding style, decomposition, and layering that is
---- the default used for compressing all components of an image  or a tile
COD - Scod   : 01                                       Binary Parameters: 00000001
COD - Progression order : 04                            Binary Parameters: 00000100
COD - Number of Layers  : 1
COD - Multiple Component Transform : 01 00000001
COD - Decomposition levels : 06
COD - CodeBlockSize : 32 x 32
COD - CodeBlock style : 00000000
COD - CodeBlock style parameter bit7 : No selective arithmetic coding bypass
COD - CodeBlock style parameter bit6 : No reset of context probabilities on coding pass boundaries
COD - CodeBlock style parameter bit5 : No termination on each coding pass
COD - CodeBlock style parameter bit4 : No vertically stripe causal context
COD - CodeBlock style parameter bit3 : No predictable termination
COD - CodeBlock style parameter bit2 : No segmentation symbols are used
COD - CodeBlock style parameter bit1 : Unknown parameter
COD - CodeBlock style parameter bit0 : Unknown parameter
COD - TransformType : 9-7 irreversible wavelet (00000000)
COD - PrecinctSize 1 : 128 x 128        (0111:0111)
COD - PrecinctSize 2 : 256 x 256        (1000:1000)
COD - PrecinctSize 3 : 256 x 256        (1000:1000)
COD - PrecinctSize 4 : 256 x 256        (1000:1000)
COD - PrecinctSize 5 : 256 x 256        (1000:1000)
COD - PrecinctSize 6 : 256 x 256        (1000:1000)
COD - PrecinctSize 7 : 256 x 256        (1000:1000)

La structure des données se décompose ainsi :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF52 Notre fameux marker
Taille 16 bits uint 0-65535 Taille - 2 octets = Taille réelle des données
Scod 8 bits bin 00000001 Code binaire avec différents paramètres par bit
Progression Order 8 bits uint 0x04 Component Position Resolution Layer (CPRL)
Number of Layer 16 bits uint 1 Nombre de layer, toujours à 1
Multiple Component Transformation 8 bits uint
Decomposition Levels 8 bits uint 0x05 en 2K
0x06 en 4K		 Nombre de décomposition ondelettes
CodeBlock Size Exponent X 8 bits uint 0x03 Nombre de l'exposant + 2 à utiliser avec le chiffre 2
CodeBlock Size Exponent Y 8 bits uint 0x03 Nombre de l'exposant + 2 à utiliser avec le chiffre 2
CodeBlock Style Parameters 8 bits bin 00000000 sera toujours à 0 (obligation DCI)
Transform Type 8 bits uint 00000000
00000001		 9-7 irreversible wavelet (D-Cinema)
5-3 reversible wavelet (IMF)
Precinct Size Exponent X 4 bits uint 0x7
0x8		 Le premier precinct
Les autres
Precinct Size Exponent Y 4 bits uint 0x7
0x8		 Le premier precinct
Les autres

QCD : Quantization default (FF5C)

Les données sont structurés de la sorte :

Ce bloc intègre les coefficients de quantification (quantization) pour le JPEG2000 :

La quantification est une méthode permettant de réduire la précision des coefficients et ainsi potentiellement gagner en place.

Voici les données parsées :

[QCD] Quantization default (0xff5c)
size: 39 bytes
data: 39 bytes readed: 227f167ee47ee47eb27700770076bc6eea6eea6ebc674c674c676450035003504557d257d25761
---- Describes the quantization default used for compressing all components not defined by a QCC marker segment.
---- The parameter values can be overridden for an individual component by a QCC marker segment in either the main or tile-part header
QCD - Sqcd (Scalar coefficient dequantization), Quantization style for all components: 00100010
QCD - Sqcd binary parameters (bit1-3): Number of guard bits 0—7: 0b001 ─➤ 1 bits
QCD - Sqcd: 0b00010 ─➤ Scalar explicit
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  0:
        ─➤ SPqcd    : 0111111100010110  (0x7f16)
        ─➤ Mantissa : 01111            : 15
        ─➤ Exponent :      11100010110 : 1814
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  1:
        ─➤ SPqcd    : 0111111011100100  (0x7ee4)
        ─➤ Mantissa : 01111            : 15
        ─➤ Exponent :      11011100100 : 1764
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  2:
        ─➤ SPqcd    : 0111111011100100  (0x7ee4)
        ─➤ Mantissa : 01111            : 15
        ─➤ Exponent :      11011100100 : 1764
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  3:
        ─➤ SPqcd    : 0111111010110010  (0x7eb2)
        ─➤ Mantissa : 01111            : 15
        ─➤ Exponent :      11010110010 : 1714
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  4:
        ─➤ SPqcd    : 0111011100000000  (0x7700)
        ─➤ Mantissa : 01110            : 14
        ─➤ Exponent :      11100000000 : 1792
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  5:
        ─➤ SPqcd    : 0111011100000000  (0x7700)
        ─➤ Mantissa : 01110            : 14
        ─➤ Exponent :      11100000000 : 1792
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  6:
        ─➤ SPqcd    : 0111011010111100  (0x76bc)
        ─➤ Mantissa : 01110            : 14
        ─➤ Exponent :      11010111100 : 1724
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  7:
        ─➤ SPqcd    : 0110111011101010  (0x6eea)
        ─➤ Mantissa : 01101            : 13
        ─➤ Exponent :      11011101010 : 1770
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  8:
        ─➤ SPqcd    : 0110111011101010  (0x6eea)
        ─➤ Mantissa : 01101            : 13
        ─➤ Exponent :      11011101010 : 1770
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band  9:
        ─➤ SPqcd    : 0110111010111100  (0x6ebc)
        ─➤ Mantissa : 01101            : 13
        ─➤ Exponent :      11010111100 : 1724
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 10:
        ─➤ SPqcd    : 0110011101001100  (0x674c)
        ─➤ Mantissa : 01100            : 12
        ─➤ Exponent :      11101001100 : 1868
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 11:
        ─➤ SPqcd    : 0110011101001100  (0x674c)
        ─➤ Mantissa : 01100            : 12
        ─➤ Exponent :      11101001100 : 1868
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 12:
        ─➤ SPqcd    : 0110011101100100  (0x6764)
        ─➤ Mantissa : 01100            : 12
        ─➤ Exponent :      11101100100 : 1892
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 13:
        ─➤ SPqcd    : 0101000000000011  (0x5003)
        ─➤ Mantissa : 01010            : 10
        ─➤ Exponent :      00000000011 : 3
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 14:
        ─➤ SPqcd    : 0101000000000011  (0x5003)
        ─➤ Mantissa : 01010            : 10
        ─➤ Exponent :      00000000011 : 3
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 15:
        ─➤ SPqcd    : 0101000001000101  (0x5045)
        ─➤ Mantissa : 01010            : 10
        ─➤ Exponent :      00001000101 : 69
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 16:
        ─➤ SPqcd    : 0101011111010010  (0x57d2)
        ─➤ Mantissa : 01010            : 10
        ─➤ Exponent :      11111010010 : 2002
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 17:
        ─➤ SPqcd    : 0101011111010010  (0x57d2)
        ─➤ Mantissa : 01010            : 10
        ─➤ Exponent :      11111010010 : 2002
QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 18:
        ─➤ SPqcd    : 0101011101100001  (0x5761)
        ─➤ Mantissa : 01010            : 10
        ─➤ Exponent :      11101100001 : 1889

La structure des données se décompose ainsi :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF5C Notre fameux marker
Taille 16 bits uint 0-65535 Taille - 2 octets = Taille réelle des données
Sqcd 8 bits bin xxx00000
xxx00001
xxx00010
000xxxxx - 111xxxxx		 Aucune quantification
Scalar implicite (la sub-band LL seulement)
Scalar explicite (toutes les sub-bands)
Nombre de bit de gardes (guard-bits) (min: 0, max: 7)
SPqcd 16 bits bin Mantisse et Exposant pour 9-7
xxxxx00000000000 — xxxxx11111111111
00000xxxxxxxxxxx — 11111xxxxxxxxxxx
Mantisse pour le coefficient de quantification
Exposant pour le coefficient de quantification

CME : Comment and extension (FF64)

Les données sont structurés de la sorte :

Ce bloc sert principalement pour l'ajout de commentaires ou de paramètres complémentaires hors scope JPEG2000 DCI. C'est un bloc totalement optionnel, certains encodeurs l'insèrent juste pour intégrer des informations sur la provenance du JPEG2000.

[CME] Comment and extension (0xff64)
size: 63 bytes
data: 63 bytes readed: 000143726561746564207769746820446f72656d69204c61627320444d533230303020534e3730303632207365727665722076312e382e302e20537263302e
---- Comment, extension and unstructured data in the header
CME - Registration values 1: Text ISO 8859-1
CME - Text: Created with Doremi Labs DMS2000 SN70062 server v1.8.0. Src0.

La structure des données se décompose ainsi :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF64 Notre fameux marker
Taille 16 bits uint 0-65535 Taille - 2 octets = Taille réelle des données
Rcme 16 bits uint 0-65535 Registration value
0 = Données binaires
1 = Données textuelles (ISO-8850-1)
1 > Réservés
Ccme variable
(blocs de 8 bits)		 bin Données binaires ou textuelles

Dans cette partie, vous ne trouverez que des données textuelles, donc nous aurons une Registration value (Rcme) toujours à 0x0001. Il suffit de lire après l'ensemble des octets jusqu'à la fin du bloc CME et de les convertir en texte.

Notez que si vous avez des données binaires (si vous utiliser du JPEG2000 en dehors du cinéma), il faudra retrouver la définition de la structure binaire dans une documentation (soit du constructeur, soit dans une norme), mais c'est hors de notre scope.

Enfin, notez que dans certaines documentations, son nom de code peut être soit CME, soit COM.

POC : Progression Order Change (FF5F)

Ce bloc de métadonnées n'est présent qu'en 4K

Les données sont structurées de la sorte :

Ce bloc définit les changements dans les différentes résolutions, les limites entre chacune des résolutions 2K/4K et de l'ordre de progression qui va évoluer dans le JPEG2000 au travers des résolutions.

Cela arrive avec l'avènement du 4K car nous aurons le 2K et le 4K dans un seul et même fichier et nous devons définir les limites de chacune et le type de Progression Order entre la première partie (2K) et la seconde (4K).

[POC] Progression Order Change (0xff5f)
size: 14 bytes
data: 14 bytes readed: 0000000106030406000001070304
---- Describes the bounds and progression order for any --------
---- progression order other than default in the codestream ----

POC - [2K] RSpoc (Resolution Start) : 0     (0x00)
POC - [2K] CSpoc (Component Start)  : 0     (0x00)
POC - [2K] LYEpoc (Layer)           : 1     (0x0001)
POC - [2K] REpoc (Resolution End)   : 6     (0x06)
POC - [2K] CEpoc (Component End)    : 3     (0x03)
POC - [2K] Ppoc (Progression Order) : 4     (0x04)

POC - [4K] RSpoc (Resolution Start) : 6     (0x06)
POC - [4K] CSpoc (Component Start)  : 0     (0x00)
POC - [4K] LYEpoc (Layer)           : 1     (0x0001)
POC - [4K] REpoc (Resolution End)   : 7     (0x07)
POC - [4K] CEpoc (Component End)    : 3     (0x03)
POC - [4K] Ppoc (Progression Order) : 4     (0x04)

La structure des données se décompose ainsi; Notez que le bloc de RSpoc à Ppoc peut être répété à l'infini :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF5F Notre fameux marker
Taille 16 bits uint 0-65535 Taille - 2 octets = Taille réelle des données
RSpoc 8 bits uint 0-255 Resolution Start
0x00 pour le 2K
0x06 pour le 4K
CSpoc 8 ou 16 bits uint 0-255 (8 bits)
0-65535 (16 bits)		 Component Start
Csiz < 257 => 8 bits
Csiz >= 257 => 16 bits
LYEpoc 16 bits uint 0-65535 Layer
REpoc 8 bits uint 0-255 Resolution End
0x06 pour le 2K
0x07 pour le 4K
CEpoc 8 ou 16 bits uint 0-255 (8 bits)
0-65535 (16 bits)		 Component End
Csiz < 257 => 8 bits
Csiz >= 257 => 16 bits
Ppoc 8 bits bin CPRL (00000011 = 0x04) Progression Order

Resolution Start (RSpoc) va définir à partir de quelle "étape" démarre la résolution pour le 2K et le 4K. Et Resolution End (REpoc) va définir la dernière étape. Ainsi, en 2K, on va partir de la résolution n°0 pour aller jusqu'à la résolution n°6; Puis, le 4K va débuter à la résolution n°6 pour monter jusqu'à la résolution n°7 (normal, entre le 2K et le 4K, c'est une seule étape car nous passons de 2048 à 4096 directement)

Pour Component Start (CSpoc) et Component End (CEpoc), c'est le même procédé, sauf qu'ici, nous aurons toujours 3 composantes pour les couleurs.

Layer Index (LYEpoc) va spécifier le nombre de couche, nous n'en aurons qu'une seule.

Pour Progression Order (Ppoc), on va définir le type d'ordre de progression (sens de lecture dans les données), on aura toujours comme valeur 0x04 pour être sur une lecture Component Position Resolution Layer (CPRL) :

Binaire Hexadecimal Nom
0000 0000 0x00 LRCP : Layer-resolution-component-position progressive
0000 0001 0x01 RLCP : Resolution-layer-component-position progressive
0000 0010 0x02 RPCL : Resolution-position-component-layer progressive
0000 0011 0x03 PCRL : Position-component-resolution-layer progressive
0000 0100 0x04 CPRL : Component-position-resolution-layer progressive

Le bloc ( RSpoc, CSpoc, LYEpoc, REpoc, CEpoc et Ppoc ) peut être répliqué plusieurs fois pour implémenter différentes résolutions. Dans notre cas, avec un 4K, nous aurons donc deux fois ce bloc, une pour le 2K et une autre pour le 4K.

TLM : Tile-part lengths, main header (FF55)

Les données sont structurées de la sorte :

Ce bloc donne des indications sur les tailles des différentes Tiles-part : les Tiles-part sont le combo d'un Start of Tile-part (SOT) et d'un Start of Data (SOD), que nous verrons plus tard.

C'est à partir de ce bloc que vous pourrez découper chaque Tile-part (Start of Tile-part + Start of Data).

Pour comprendre un peu le jeu des relations entre TLM, SOT et SOD, voyons un schéma simple :

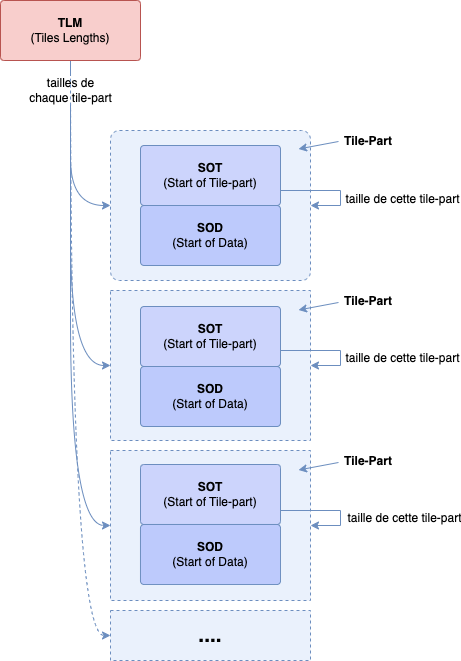
TLM est un peu la porte d'entrée des différents SOT+SOD.

Les Start of Tile-part (SOT) respectent la structure d'un KLV, vous aurez donc une taille mais que pour sa propre partie (la taille d'un SOT tourne autour de la dizaine de bytes) sans prendre en compte son Start of Data (SOD).

Les Start of Data (SOD) ne respectent pas la structure d'un KLV, nous n'aurons donc aucune taille : on saute directement aux données brutes.

Nous devons donc nous retourner :

Voici un exemple de données pour un Tile-part Lengths sur un 4K (nous aurons 6 Tile-parts; en 2K, nous en aurions que 3) :

[TLM] Tile-part lengths, main header          (FF55)
size: 32 bytes
data: 32 bytes readed: 005000000000be000000003b000000003b000000007e000000007e000000007e
---- Describes the length of every tile-part in the codestream
---- Each tile-part’s length is measured from the first byte of the SOT marker segment
---- to the end of the data of that tile-part. The value of each individual tile-part length in the TLM
---- marker segment is the same as the value in the corresponding Psot in the SOT marker segment.
TLM - Ztlm: Index of this marker segment: 0
TLM - Stlm: Size of the Ttlm and Ptlm parameters: 01010000
TLM - Stlm Bit-Parameters: SP = 1; Ptlm parameter 32 bits
TLM - Stlm Bit-Parameters: ST = 1; Ttlm parameter 8 bits
TLM - Ttlm -    Tile number of tile-part 1: 0
TLM - Ptlm - Length SOT+SOD of tile-part 1: 190 bytes
TLM - Ttlm -    Tile number of tile-part 2: 0
TLM - Ptlm - Length SOT+SOD of tile-part 2: 59 bytes
TLM - Ttlm -    Tile number of tile-part 3: 0
TLM - Ptlm - Length SOT+SOD of tile-part 3: 59 bytes
TLM - Ttlm -    Tile number of tile-part 4: 0
TLM - Ptlm - Length SOT+SOD of tile-part 4: 126 bytes
TLM - Ttlm -    Tile number of tile-part 5: 0
TLM - Ptlm - Length SOT+SOD of tile-part 5: 126 bytes
TLM - Ttlm -    Tile number of tile-part 6: 0
TLM - Ptlm - Length SOT+SOD of tile-part 6: 126 bytes

Le paramètre Stlm est un code binaire qui va déterminer la taille en bit des paramètres Ttlm et Ptlm. Par chance, notre paramètre sera toujours le même, nous aurons une taille de Ttlm de 8 bits et une taille de Ptlm de 32 bits.

La structure des données se décompose ainsi. Le bloc Ttlm + Ptlm peut être répété plusieurs fois pour couvrir chaque Tile.

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF55 Notre fameux marker
Taille 16 bits uint 0-65535 Taille - 2 octets = Taille réelle des données
Ztlm 8 bits bin 0 Index du segment (on en aura qu'un)
Stlm 8 bits bin 01010000 Code binaire qui va déterminer la taille de Ttlm et Ptlm
Ttlm 8 bits uint 0 Numéro de la tile (on en aura qu'une)
Ptlm 32 bits uint 0-4294967295 Taille de la Tile-part (SOT+SOD)

Pour Stlm, le code binaire va respecter ce type d'encodage :

Binaire Description
xx00xxxx Ttlm de 0 bits, Aucun Ptlm
xx01xxxx Ttlm de 8 bits
xx10xxxx Ttlm de 16 bits
x0xxxxxx Ptlm de 16 bits
x1xxxxxx Ptlm de 32 bits

A partir de là, vous saurez comment lire les données Ttlm et Ptlm.
(dans notre cas, nous serons toujours à 8+32 bits, donc un code binaire de 01010000)

SOT : Start of tile-part (FF90)

Les données sont structurées de la sorte :

Et au niveau de la structure d'un JPEG2000 vous aurez plusieurs Start of Tile-part (SOT) l'un à la suite de l'autre :

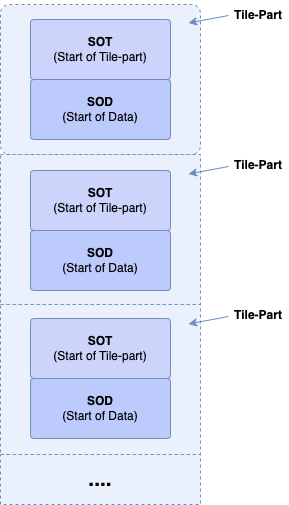
Les Start of Tile-part (SOT) sont des blocs de métadonnées donnant des indications sur les Start of Data (SOD) qui leurs sont rattachés. SOT et SOD font partie de ce qu'on appelle une Tile-part :

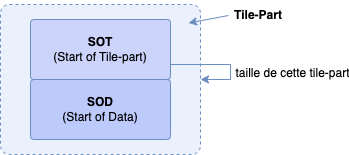
Vous aurez un Start of Tile-part (SOT) par Tiles-part :

Le Start of Tile-part (SOT) n'a pas d'autre utilité que de définir le Start of Data (SOD) qui va suivre chaque Start of Tile-part (SOT).

Voici les données des 6 différents Start of Tile-part (SOT) d'un 4K :

# --- SOT du Tile n°1 ---
[SOT] Start of tile-part (FF90)
size: 8 bytes
data: 8 bytes readed: 0000000000be0006
SOT - Isot, Tile number           : 0
SOT - Psot, Length of SOT+SOD     : 190
SOT - TPsot, Tile-part number     : 0
SOT - TNsot, Number of tile-parts : 6

# --- SOT du Tile n°2 ---
[SOT] Start of tile-part (FF90)
size: 8 bytes
data: 8 bytes readed: 00000000003b0106
SOT - Isot, Tile number           : 0
SOT - Psot, Length of SOT+SOD     : 59
SOT - TPsot, Tile-part number     : 1
SOT - TNsot, Number of tile-parts : 6

# --- SOT du Tile n°3 ---
[SOT] Start of tile-part (FF90)
size: 8 bytes
data: 8 bytes readed: 00000000003b0206
SOT - Isot, Tile number           : 0
SOT - Psot, Length of SOT+SOD     : 59
SOT - TPsot, Tile-part number     : 2
SOT - TNsot, Number of tile-parts : 6

# --- SOT du Tile n°4 ---
[SOT] Start of tile-part (FF90)
size: 8 bytes
data: 8 bytes readed: 00000000007e0306
SOT - Isot, Tile number           : 0
SOT - Psot, Length of SOT+SOD     : 126
SOT - TPsot, Tile-part number     : 3
SOT - TNsot, Number of tile-parts : 6

# --- SOT du Tile n°5 ---
[SOT] Start of tile-part (FF90)
size: 8 bytes
data: 8 bytes readed: 00000000007e0406
SOT - Isot, Tile number           : 0
SOT - Psot, Length of SOT+SOD     : 126
SOT - TPsot, Tile-part number     : 4
SOT - TNsot, Number of tile-parts : 6

# --- SOT du Tile n°6 ---
[SOT] Start of tile-part (FF90)
size: 8 bytes
data: 8 bytes readed: 00000000007e0506
SOT - Isot, Tile number           : 0
SOT - Psot, Length of SOT+SOD     : 126
SOT - TPsot, Tile-part number     : 5
SOT - TNsot, Number of tile-parts : 6

Avec le paramètre Psot (taille SOT+SOD), vous serez capable de déterminer la taille du Start of Data (SOD) et ainsi pouvoir récupérer les données brutes de la composante de notre image.

La structure des données se décompose ainsi :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF90 Notre fameux marker
Taille 16 bits uint 0-65535
10		 Taille - 2 octets = Taille réelle des données
Sa taille est fixe
Isot 16 bits uint 0 Numéro de la tile (sera toujours à 0)
Psot 32 bits uint 0-4294967295 Taille en octets de la tile-part (SOT+SOD)
TPsot 8 bits uint 0-255 Numéro du tile-part
TNsot 8 bits uint 3 en 2K
6 en 4K		 Nombre de tile-parts

Le Start of Tile-part possède un Length mais sa taille est fixée à 10.

À noter que certaines recommandations 14 préconisent que le premier SOT doit être en dessous des 255 octets afin de garder une compatibilité avec certains matériels. Autrement dit, les métadonnées essentiels (SIZ+COD+QCD+POC+TLM) doivent tenir en dessous des 255 octets. Il faudra donc ne pas abuser des markers non-essentiels dans l'entête, et surtout, ne pas utiliser le marker Comment and Extension (CME) ou soit de l'utiliser avec parcimonie.

SOD : Start of data (FF93)

Les données sont structurées de la sorte :

Ce bloc intègre QUE les données de notre image.

Le Start of Data ne respecte pas une structure de type KLV, il ne possède aucun code pour sa taille. Pour déterminer sa taille, nous avons besoin soit de lire le Tiles-Lengths (TLM), soit de lire le Start of Tile-part (SOT) qui sera au dessus de lui et incorpore le paramètre Psot qui est la taille du SOT+SOD, on devra donc faire un petit calcul pour retrancher la taille du SOT pour avoir - enfin - la taille du SOD.

Vous aurez un Start of Data (SOD) par Tiles-part :

Le marker SOD est le dernier marker de la Tile-part et il n'y a qu'un seul SOD par Tile-part. Enfin, un SOD est un multiple de 8 bits, si ce n'est pas le cas, on rajoutera un padding à la fin avant de passer au prochain Start of Tile (SOT) ou au End of Codestream (EOC).

# --- Data of Tile-part 1 ---
[SOD] Start of data      (FF93)
data: 176 bytes readed: eff07ffe0fc0115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c8080808080808080808080808080808080808080808080808080808080808080808080808080808080808080

# --- Data of Tile-part 2 ---
[SOD] Start of data      (FF93)
data: 45 bytes readed: 808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080

# --- Data of Tile-part 3 ---
[SOD] Start of data      (FF93)
data: 45 bytes readed: 808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080

# --- Data of Tile-part 4 ---
[SOD] Start of data      (FF93)
data: 112 bytes readed: 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080

# --- Data of Tile-part 5 ---
[SOD] Start of data      (FF93)
data: 112 bytes readed: 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080

# --- Data of Tile-part 6 ---
[SOD] Start of data      (FF93)
data: 112 bytes readed: 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080

Les données présentées ne sont pas forcément pertinentes car nous n'avons qu'une énorme image noire :)

La structure des données se décompose ainsi :

Nom de code Taille Type Valeurs Description
Marker 16 bits bin 0xFF55 Notre fameux marker
Data x * 8 bits bin ... Les données brutes de notre image (par composante)

EOC : End of codestream (FFD9)

Un fichier JPEG2000 se termine par le code 0xFFD9.

Spécifications et obligations du JPEG2000 DCI

Contraintes de tailles & bitrates :

Pour un contenu classique (2K, 4K, SDR), la limitation de bande-passante (bitrate) est de 250 Mb/s :

Les contraintes de tailles 15 :

- Taille par frame
(3 composantes + Headers)		 Taille maximale
composante par frame
2K - 24 fps 1.302.083 octets
(1.3 Mo)		 1.041.666 octets 16
(1.04 Mo)
2K - 48 fps
(HFR ou 3D)		 651.041 octets
(0.65 Mo)		 520.833 octets 17
(0.52 Mo)
4K 1.302.083 octets
(1.3 Mo)		 1.041.666 octets
(1.04 Mo)

Pour le HFR, 3D et HDR, la limitation de bande-passante (bitrate) est à 500 Mb/s 18

Et en archivage / IMF ? En archivage, le bitdepth sera à 12 ou 16 bits, sans perte avec le wavelet 5/3 et du Reversible Color Transformation (ICT), le bitrate peut dépasser 1 Gbit/s

Prévoyez de ne pas compresser les JPEG2000 à la limite de leur bande-passante, vous pourriez, par inadvertance, dépasser cette limite sans vous en rendre compte, consultez le chapitre Cryptographie, paragraphe Le padding cryptographique et la limite de la bande passante pour en savoir plus.

Codes et techniques

Voici différentes méthodes pour manipuler du JPEG2000.

Lire et parser un JPEG2000 soi-même

Tout d'abord, les codes des markers ne sont pas protégés, cela veut dire que leurs codes hexadécimaux peuvent se retrouver n'importe où dans le fichier et d'autant plus dans les données de l'image. Ne vous amusez pas à parser un JPEG2000 en essayant de trouver ces codes et en imaginant pouvoir trouver un marker comme cela : vous allez au-devant des problèmes.

N'oubliez pas que hormis quelques blocs spécifiques, certains blocs peuvent être optionnels. N'estimez pas qu'après tel bloc, vous aurez obligatoirement tel autre bloc. Basez-vous uniquement sur les codes des markers pour déterminer le type de bloc et donc le type de données.

Focalisez-vous sur le marker du premier bloc - celui juste après le marker obligatoire Start of Codestream (SOC); Et à partir de là, si vous lisez sa taille, vous trouverez le second marker de votre second bloc, et ainsi de suite.

En langage plus technique, faites un seek(2) pour bypasser le marker SOC - qui nous est inutile là - afin d'arriver directement au premier marker du premier bloc. Faites un read(2) pour lire le premier marker de votre premier bloc, puis faites de nouveau un read(2) pour lire la taille de votre bloc. N'oubliez pas que la taille récupérée incorpore la taille des données et la taille de votre taille, il faudra donc retrancher 2 octets à la valeur récupérée dans la taille avant d'effectuer une lecture des données avec un read(length - 2). Si vous faites de nouveau un read(2), vous trouverez le marker suivant de votre bloc suivant, et ainsi de suite :

with open("black_4k.j2c", "rb") as file:

    # On va lire le premier marker de notre fichier (SOC)
    marker_soc = file.read(2)
    print(f"SOC: {marker_soc.hex()}")

    # On va boucler sur l'ensemble des KLV
    while True:

        # On va lire chaque marker
        marker = file.read(2)

        # Aucun marker, on arrête de lire
        if not marker:
            break

        # On lit la taille (2 octets)
        length = file.read(2)

        # On convertit en int
        length = int.from_bytes(length, byteorder='big')

        # On n'oublie pas d'enlever les 2 octets en trop
        length -= 2

        # On lit les données
        data = file.read(length)

        print(f"{marker.hex()} : {length} bytes = {data.hex()}")

Et si on exécute notre programme :

SOC: ff4f
ff51 : 45 bytes = 000400001000000006b4000000000000000000001000000006b4000000000000000000030b01010b01010b0101
ff52 : 17 bytes = 0104000101060303000077888888888888
ff5c : 39 bytes = 227f167ee47ee47eb27700770076bc6eea6eea6ebc674c674c676450035003504557d257d25761
ff64 : 63 bytes = 000143726561746564207769746820446f72656d69204c61627320444d533230303020534e3730303632207365727665722076312e382e302e20537263302e
ff5f : 14 bytes = 0000000106030406000001070304
ff55 : 32 bytes = 005000000000be000000003b000000003b000000007e000000007e000000007e
ff90 : 08 bytes = 0000000000be0006
ff93 : 61422 bytes = 7ffe0fc0115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c8080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ff90000a00000000003b0106ff93808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ff90000a00000000003b0206ff93808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ff90000a00000000007e0306ff9380808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ff90000a00000000007e0406ff9380808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ff90000a00000000007e0506ff9380808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ffd9

Nous avons nos principaux éléments... sauf pour le dernier qui semble bizarre.

Et oui, le ff90 et ff93 sont respectivement nos Start of Tile-part (SOT) et Start of Data (SOD), mais souvenez-vous que :

C'est parce que notre SOD (FF93) ne possède pas de Length que notre dernier KLV semble corrompu : notre programme simpliste a essayé de lire les 16 premiers bits du SOD en supposant que c'était sa taille.

Pour corriger ce problème, le plus simple est de lire votre Start of Tile-part puis de récupérer la métadonnée Psot qui vous donnera des indications sur la taille de votre bloc Start of Data : Psot intègre la taille de la Tile-part (SOT+SOD).

Si vous lisez Start of Tile-part avec son Start of Data, vous tomberez sur le prochain Start of Tile-part, et ainsi de suite.

Nous allons ajouter un patch quick & dirty pour comprendre la logique :

# ----------------------------------------------------------------------
# A ajouter après :
#        print(f"{marker.hex()} : {length} bytes = {data.hex()}")
# ----------------------------------------------------------------------

        # Le début d'un Tile-part (SOT)
        # Nous allons donc essayer de lire le Psot
        # qui intègre la taille de la tile-part (SOT+SOD)
        if marker.hex() == "ff90":

            # Tile-part Length se trouve à l'offset 16
            # et à une taille de 32 bits
            tilepart_length = data[2:6]

            # On convertit en int
            tilepart_length = int.from_bytes(tilepart_length, byteorder='big')

            # tilePart = SOT+SOD
            # keyLength = 16 bits
            # lengthLength = 16 bits
            # (tilePartLength - SOTLength - (keyLength + lengthLength)
            SOD_length = (tilepart_length - len(data) - 4)

            # On lit les données du SOD (avec son marker)
            SOD_data = file.read(SOD_length)

            # On affiche le marker de SOD (16 bits), sa taille et ses données
            print(f"{SOD_data[0:2].hex()} : {len(SOD_data)} bytes = {SOD_data[2:].hex()}")

Si on trouve le marker du Start of Tile-part (SOT), on va lire dans ses données et en extraire le Psot qui va nous donner la taille de SOT+SOD. De là, nous effectuons une simple soustraction pour supprimer toutes les données inutiles puis nous lisons les données de SOD.

Avec notre file.read(SOD_length), le pointeur dans le fichier va être décalé et nous allons retomber sur le prochain Start of Tile-part (SOT)

Voyons ce qu'il se passe :

SOC: ff4f
ff51 : 45 bytes = 000400001000000006b4000000000000000000001000000006b4000000000000000000030b01010b01010b0101
ff52 : 17 bytes = 0104000101060303000077888888888888
ff5c : 39 bytes = 227f167ee47ee47eb27700770076bc6eea6eea6ebc674c674c676450035003504557d257d25761
ff64 : 63 bytes = 000143726561746564207769746820446f72656d69204c61627320444d533230303020534e3730303632207365727665722076312e382e302e20537263302e
ff5f : 14 bytes = 0000000106030406000001070304
ff55 : 32 bytes = 005000000000be000000003b000000003b000000007e000000007e000000007e
ff90 : 8 bytes = 0000000000be0006
ff93 : 178 bytes = eff07ffe0fc0115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c8080808080808080808080808080808080808080808080808080808080808080808080808080808080808080
ff90 : 8 bytes = 00000000003b0106
ff93 : 47 bytes = 808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080
ff90 : 8 bytes = 00000000003b0206
ff93 : 47 bytes = 808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080
ff90 : 8 bytes = 00000000007e0306
ff93 : 114 bytes = 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080
ff90 : 8 bytes = 00000000007e0406
ff93 : 114 bytes = 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080
ff90 : 8 bytes = 00000000007e0506
ff93 : 114 bytes = 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080
Traceback (most recent call last):
  File "/private/tmp/test.py", line 27, in <module>
    data = file.read(length)
ValueError: read length must be non-negative or -1

Nous avons bien nos différentes 6 tile-parts (SOT+SOD) de notre fichier 4K !

Sauf que nous avons un petit plantage à la fin... Et oui, c'est notre End of Codestream (EOC), vu qu'il n'y a plus de données, on rajoutera un petit patch simple de 2 lignes pour compenser rapidement ce problème :

###       # On n'oublie pas d'enlever les 2 octets en trop
###       length -= 2

++        if length < 0:
++            break

###       # On lit les données
###       data = file.read(length)

Notre programme s'arrêtera s'il n'y a aucune donnée à lire.

Vous retrouverez ce petit programme jpeg2000-parser-lite.py à tester avec l'image black_4k.j2c.

Avec ceci, vous avez déjà une partie de l'analyse du JPEG2000, il faudra maintenant analyser chaque portion de données dans chaque bloc pour en extraire les métadonnées.

Vous retrouverez jpeg2000-parser.py, son grand frère un peu plus complet qui parse justement les métadonnées complètes d'un JPEG2000 DCI :

$ ./jpeg2000-parser.py analyse/black_4k.j2c read analyse/black_4k.j2c [SOC] Start of codestream (FF4F) [SIZ] Image and tile size (FF51) offs: 2 size: 45 bytes data: 45 bytes readed: 000400001000000006b4000000000000000000001000000006b4000000000000000000030b01010b01010b0101 ---- Provides information about the uncompressed image such as the width and height of the reference grid, ---- the width and height of the tiles, the number of components, component bit depth, ---- and the separation of component samples with respect to the reference grid SIZ - rsiz : Profile 4 SIZ - Xsiz : 4096 px SIZ - Ysiz : 1716 px SIZ - XOsiz : 0 px SIZ - YOsiz : 0 px SIZ - XTsiz : 4096 px SIZ - YTsiz : 1716 px SIZ - XTOsiz : 0 px SIZ - YTOsiz : 0 px SIZ - Csiz : 3 components SIZ - Component 1 - ssizDepth : 11 ─➤ 12 bits Components Parameters (00001011) SIZ - Component 1 - xRsiz : 1 bit(s) Horizontal separation of a sample SIZ - Component 1 - yRsiz : 1 bit(s) Vertical separation of a sample SIZ - Component 2 - ssizDepth : 11 ─➤ 12 bits Components Parameters (00001011) SIZ - Component 2 - xRsiz : 1 bit(s) Horizontal separation of a sample SIZ - Component 2 - yRsiz : 1 bit(s) Vertical separation of a sample SIZ - Component 3 - ssizDepth : 11 ─➤ 12 bits Components Parameters (00001011) SIZ - Component 3 - xRsiz : 1 bit(s) Horizontal separation of a sample SIZ - Component 3 - yRsiz : 1 bit(s) Vertical separation of a sample [COD] Coding style default (FF52) offs: 51 size: 17 bytes data: 17 bytes readed: 0104000101060303000077888888888888 ---- Describes the coding style, decomposition, and layering that is ---- the default used for compressing all components of an image or a tile COD - Scod : 01 Binary Parameters: 00000001 COD - Progression order : 04 Binary Parameters: 00000100 COD - Number of Layers : 1 COD - Multiple Component Transform : 01 00000001 COD - Decomposition levels : 6 COD - CodeBlockSize : 32 x 32 COD - CodeBlock style : 00000000 COD - CodeBlock style parameter bit7 : No selective arithmetic coding bypass COD - CodeBlock style parameter bit6 : No reset of context probabilities on coding pass boundaries COD - CodeBlock style parameter bit5 : No termination on each coding pass COD - CodeBlock style parameter bit4 : No vertically stripe causal context COD - CodeBlock style parameter bit3 : No predictable termination COD - CodeBlock style parameter bit2 : No segmentation symbols are used COD - CodeBlock style parameter bit1 : Unknown parameter COD - CodeBlock style parameter bit0 : Unknown parameter COD - TransformType : 9-7 irreversible wavelet (00000000) COD - PrecinctSize 1 : 128 x 128 (0111:0111) COD - PrecinctSize 2 : 256 x 256 (1000:1000) COD - PrecinctSize 3 : 256 x 256 (1000:1000) COD - PrecinctSize 4 : 256 x 256 (1000:1000) COD - PrecinctSize 5 : 256 x 256 (1000:1000) COD - PrecinctSize 6 : 256 x 256 (1000:1000) COD - PrecinctSize 7 : 256 x 256 (1000:1000) [QCD] Quantization default (FF5C) offs: 72 size: 39 bytes data: 39 bytes readed: 227f167ee47ee47eb27700770076bc6eea6eea6ebc674c674c676450035003504557d257d25761 ---- Describes the quantization default used for compressing all components not defined by a QCC marker segment. ---- The parameter values can be overridden for an individual component by a QCC marker segment in either the main or tile-part header QCD - Sqcd (Scalar coefficient dequantization), Quantization style for all components: 00100010 QCD - Sqcd binary parameters (bit1-3): Number of guard bits 0—7: 0b001 ─➤ 1 bits QCD - Sqcd: 0b00010 ─➤ Scalar explicit QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 0: ─➤ SPqcd : 0111111100010110 (0x7f16) ─➤ Mantissa : 01111 : 15 ─➤ Exponent : 11100010110 : 1814 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 1: ─➤ SPqcd : 0111111011100100 (0x7ee4) ─➤ Mantissa : 01111 : 15 ─➤ Exponent : 11011100100 : 1764 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 2: ─➤ SPqcd : 0111111011100100 (0x7ee4) ─➤ Mantissa : 01111 : 15 ─➤ Exponent : 11011100100 : 1764 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 3: ─➤ SPqcd : 0111111010110010 (0x7eb2) ─➤ Mantissa : 01111 : 15 ─➤ Exponent : 11010110010 : 1714 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 4: ─➤ SPqcd : 0111011100000000 (0x7700) ─➤ Mantissa : 01110 : 14 ─➤ Exponent : 11100000000 : 1792 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 5: ─➤ SPqcd : 0111011100000000 (0x7700) ─➤ Mantissa : 01110 : 14 ─➤ Exponent : 11100000000 : 1792 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 6: ─➤ SPqcd : 0111011010111100 (0x76bc) ─➤ Mantissa : 01110 : 14 ─➤ Exponent : 11010111100 : 1724 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 7: ─➤ SPqcd : 0110111011101010 (0x6eea) ─➤ Mantissa : 01101 : 13 ─➤ Exponent : 11011101010 : 1770 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 8: ─➤ SPqcd : 0110111011101010 (0x6eea) ─➤ Mantissa : 01101 : 13 ─➤ Exponent : 11011101010 : 1770 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 9: ─➤ SPqcd : 0110111010111100 (0x6ebc) ─➤ Mantissa : 01101 : 13 ─➤ Exponent : 11010111100 : 1724 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 10: ─➤ SPqcd : 0110011101001100 (0x674c) ─➤ Mantissa : 01100 : 12 ─➤ Exponent : 11101001100 : 1868 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 11: ─➤ SPqcd : 0110011101001100 (0x674c) ─➤ Mantissa : 01100 : 12 ─➤ Exponent : 11101001100 : 1868 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 12: ─➤ SPqcd : 0110011101100100 (0x6764) ─➤ Mantissa : 01100 : 12 ─➤ Exponent : 11101100100 : 1892 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 13: ─➤ SPqcd : 0101000000000011 (0x5003) ─➤ Mantissa : 01010 : 10 ─➤ Exponent : 00000000011 : 3 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 14: ─➤ SPqcd : 0101000000000011 (0x5003) ─➤ Mantissa : 01010 : 10 ─➤ Exponent : 00000000011 : 3 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 15: ─➤ SPqcd : 0101000001000101 (0x5045) ─➤ Mantissa : 01010 : 10 ─➤ Exponent : 00001000101 : 69 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 16: ─➤ SPqcd : 0101011111010010 (0x57d2) ─➤ Mantissa : 01010 : 10 ─➤ Exponent : 11111010010 : 2002 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 17: ─➤ SPqcd : 0101011111010010 (0x57d2) ─➤ Mantissa : 01010 : 10 ─➤ Exponent : 11111010010 : 2002 QCD - SPqcd (Exponent+Mantissa), Quantization step size value sub-band 18: ─➤ SPqcd : 0101011101100001 (0x5761) ─➤ Mantissa : 01010 : 10 ─➤ Exponent : 11101100001 : 1889 [CME] Comment and extension (FF64) offs: 115 size: 63 bytes data: 63 bytes readed: 000143726561746564207769746820446f72656d69204c61627320444d533230303020534e3730303632207365727665722076312e382e302e20537263302e ---- Comment, extension and unstructured data in the header CME - Registration values 1: Text ISO 8859-1 CME - Text: Created with Doremi Labs DMS2000 SN70062 server v1.8.0. Src0. [POC] Progression Order Change (FF5F) offs: 182 size: 14 bytes data: 14 bytes readed: 0000000106030406000001070304 ---- Describes the bounds and progression order for any progression order other than default in the codestream ---- POC - [2K] RSpoc (Resolution Start) : 0 (0x00) POC - [2K] CSpoc (Component Start) : 0 (0x00) POC - [2K] LYEpoc (Layer) : 1 (0x0001) POC - [2K] REpoc (Resolution End) : 6 (0x06) POC - [2K] CEpoc (Component End) : 3 (0x03) POC - [2K] Ppoc (Progression Order) : 4 (0x04) POC - [4K] RSpoc (Resolution Start) : 6 (0x06) POC - [4K] CSpoc (Component Start) : 0 (0x00) POC - [4K] LYEpoc (Layer) : 1 (0x0001) POC - [4K] REpoc (Resolution End) : 7 (0x07) POC - [4K] CEpoc (Component End) : 3 (0x03) POC - [4K] Ppoc (Progression Order) : 4 (0x04) [TLM] Tile-part lengths, main header (FF55) offs: 200 size: 32 bytes data: 32 bytes readed: 005000000000be000000003b000000003b000000007e000000007e000000007e ---- Describes the length of every tile-part in the codestream ---- Each tile-part’s length is measured from the first byte of the SOT marker segment ---- to the end of the data of that tile-part. The value of each individual tile-part length in the TLM ---- marker segment is the same as the value in the corresponding Psot in the SOT marker segment. TLM - Ztlm: Index of this marker segment: 0 TLM - Stlm: Size of the Ttlm and Ptlm parameters: 01010000 TLM - Stlm Bit-Parameters: SP = 1; Ptlm parameter 32 bits TLM - Stlm Bit-Parameters: ST = 1; Ttlm parameter 8 bits TLM - Ttlm - Tile number of tile-part 1: 0 TLM - Ptlm - Length SOT+SOD of tile-part 1: 190 bytes TLM - Ttlm - Tile number of tile-part 2: 0 TLM - Ptlm - Length SOT+SOD of tile-part 2: 59 bytes TLM - Ttlm - Tile number of tile-part 3: 0 TLM - Ptlm - Length SOT+SOD of tile-part 3: 59 bytes TLM - Ttlm - Tile number of tile-part 4: 0 TLM - Ptlm - Length SOT+SOD of tile-part 4: 126 bytes TLM - Ttlm - Tile number of tile-part 5: 0 TLM - Ptlm - Length SOT+SOD of tile-part 5: 126 bytes TLM - Ttlm - Tile number of tile-part 6: 0 TLM - Ptlm - Length SOT+SOD of tile-part 6: 126 bytes [SOT] Start of tile-part (FF90) offs: 236 size: 8 bytes data: 8 bytes readed: 0000000000be0006 ---- Marks the beginning of a tile-part and the index of its tile within a codestream ---- The tile-parts of a tile shall appear in order (see TPsot) in the codestream ---- but not necessarily consecutively. SOT - Isot, Tile number : 0 SOT - Psot, Length of SOT+SOD : 190 SOT - TPsot, Tile-part number : 0 SOT - TNsot, Number of tile-parts : 6 [SOD] Start of data (FF93) data: 176 bytes : eff07ffe0fc0115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c115054afff5574bcab4000000000000c2425ff69dc40000000000309097fe4a5400000000061212ffc94a8000000000c2425ff494a8000000000c2425ffd3c8080808080808080808080808080808080808080808080808080808080808080808080808080808080808080 [SOT] Start of tile-part (FF90) offs: 426 size: 8 bytes data: 8 bytes readed: 00000000003b0106 ---- Marks the beginning of a tile-part and the index of its tile within a codestream ---- The tile-parts of a tile shall appear in order (see TPsot) in the codestream ---- but not necessarily consecutively. SOT - Isot, Tile number : 0 SOT - Psot, Length of SOT+SOD : 59 SOT - TPsot, Tile-part number : 1 SOT - TNsot, Number of tile-parts : 6 [SOD] Start of data (FF93) data: 45 bytes : 808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080 [SOT] Start of tile-part (FF90) offs: 485 size: 8 bytes data: 8 bytes readed: 00000000003b0206 ---- Marks the beginning of a tile-part and the index of its tile within a codestream ---- The tile-parts of a tile shall appear in order (see TPsot) in the codestream ---- but not necessarily consecutively. SOT - Isot, Tile number : 0 SOT - Psot, Length of SOT+SOD : 59 SOT - TPsot, Tile-part number : 2 SOT - TNsot, Number of tile-parts : 6 [SOD] Start of data (FF93) data: 45 bytes : 808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080 [SOT] Start of tile-part (FF90) offs: 544 size: 8 bytes data: 8 bytes readed: 00000000007e0306 ---- Marks the beginning of a tile-part and the index of its tile within a codestream ---- The tile-parts of a tile shall appear in order (see TPsot) in the codestream ---- but not necessarily consecutively. SOT - Isot, Tile number : 0 SOT - Psot, Length of SOT+SOD : 126 SOT - TPsot, Tile-part number : 3 SOT - TNsot, Number of tile-parts : 6 [SOD] Start of data (FF93) data: 112 bytes : 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080 [SOT] Start of tile-part (FF90) offs: 670 size: 8 bytes data: 8 bytes readed: 00000000007e0406 ---- Marks the beginning of a tile-part and the index of its tile within a codestream ---- The tile-parts of a tile shall appear in order (see TPsot) in the codestream ---- but not necessarily consecutively. SOT - Isot, Tile number : 0 SOT - Psot, Length of SOT+SOD : 126 SOT - TPsot, Tile-part number : 4 SOT - TNsot, Number of tile-parts : 6 [SOD] Start of data (FF93) data: 112 bytes : 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080 [SOT] Start of tile-part (FF90) offs: 796 size: 8 bytes data: 8 bytes readed: 00000000007e0506 ---- Marks the beginning of a tile-part and the index of its tile within a codestream ---- The tile-parts of a tile shall appear in order (see TPsot) in the codestream ---- but not necessarily consecutively. SOT - Isot, Tile number : 0 SOT - Psot, Length of SOT+SOD : 126 SOT - TPsot, Tile-part number : 5 SOT - TNsot, Number of tile-parts : 6 [SOD] Start of data (FF93) data: 112 bytes : 80808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080 [EOC] End of codestream (FFD9)

Les outils externes pour manipuler du JPEG2000

OpenJPEG

OpenJPEG est la librairie de référence pour le JPEG et ses dérivés et notamment le JPEG2000 dans le milieu opensource.

Compilation de OpenJPEG :

$ git clone "https://github.com/uclouvain/openjpeg.git"
$ cd "openjpeg"
$ mkdir "build"
$ cd "build"
$ cmake .. -DCMAKE_BUILD_TYPE=Release
$ make
$ ls ./bin/opj_*
./bin/opj_compress
./bin/opj_decompress
./bin/opj_dump

Si vous ne voulez pas compiler, vous pouvez télécharger des versions pour Linux, MacOS et Windows : https://github.com/uclouvain/openjpeg/releases

Sous Linux (Debian/Ubuntu) :

$ apt-get install openjpeg

Sous MacOS :

brew install openjpeg
ou
port install openjpeg

Pour compresser (méthode easy) :

# Compression 2K image par image
opj_compress -cinema2K 24 -i "2048x1080.tif" -o "2048x1080.j2c"

# Compression 4K image par image
opj_compress -cinema4K -i "4096x2160.tif" -o "4096x2160.j2c"

# Compression depuis un répertoire
opj_compress -cinema2K 24 -ImgDir input/ -OutFor J2C

Notez que depuis la version 2.4.0, OpenJPEG supporte aussi les profiles IMF.

Pour analyser :

opj_dump -i frame.j2c

Kakadu

CAUTION - NOT TESTED YET

Kakadu est un tooklit de développement JPEG2000 de référence et très performant.

Version 2K en 24 FPS :

kdu_compress \
    -i "frame_2k.tif" \
    -o "frame_2k.jp2" \
    Sprofile=CINEMA2K \
    Creslengths=1041666 \
    Creslengths:C0=833333 \
    Creslengths:C1=375000 \
    Cagglengths:C2=1

Le chiffre 1041666 correspond à la limite que nous avons vu plus haut.

Le paramètre Creslengths effectue une constrainte sur la taille (en octets) à propos des paquets JPEG2000 (cela inclut les packet bodies et les packet headers, à l'exclusion du main header ou tile-part header sizes)

Version 4K en 24-60 FPS :

kdu_compress \
    -i "frame_4k.tif" \
    -o "frame_4k.jp2" \
    Sprofile=CINEMA4K \
    Creslengths=1302083 \ 
    Creslengths:C0=1302083,1041666 \
    Creslengths:C1=1302083,1041666 \
    Creslengths:C2=1302083,1041666

Les chiffres 1302083 et 1041666 correspondent aux limites que nous avons vu plus haut.

Legacy Compatibility for Dolby Player :

kdu_compress \
    -i "frame_2K.tif" \
    -o "frame_2K.j2c" \
    Sprofile=CINEMA2K \
    Creslengths=1301827 \
    Creslengths:C0=1041410 \
    Creslengths:C1=1041410 \
    Creslengths:C2=1041410 \
    -fprec 12M \
    -no_info

kdu_compress \
    -i "frame_4K.tif" \
    -o "frame_4K.j2c" \
    Sprofile=CINEMA4K \
    Creslengths=1301827 \
    Creslengths:C0=1301827,1041410 \
    Creslengths:C1=1301827,1041410 \
    Creslengths:C2=1301827,1041410 \
    -fprec 12M \
    -no_info

Autres

Analyse des J2C avec la librairie jpylyzer sous Python : 

#!/usr/bin/env python3

import sys
from jpylyzer import boxvalidator as jpylyzer

def walk(elements, padding=0):

       for property in elements:

               # --- read each sections of properties ---
               if property.tag and property.text is None:
                       yield "{padding}[{tag:s}]".format(
                               padding = '    ' * padding,
                               tag = property.tag
                       )

                       # recursive properties
                       yield from walk(property, padding=padding+1)

               # --- read each property ---
               if property.tag and property.text:
                       yield "{padding}{tag:15s} : {text:<5s}".format(
                               padding = '    ' * padding,
                               tag = property.tag,
                               text = str(property.text)
                       )

def j2c_metadatas(data):
       results = jpylyzer.BoxValidator("contiguousCodestreamBox", data).validate()
       return walk(results.characteristics)

for filename in sys.argv[1:]:
       with open(filename, "rb") as file:
               print(f"open {filename}")
               for field in j2c_metadatas(file.read()):
                       print(field)

Note: A l'heure actuelle, cette librairie est moins complète que notre parseur maison pour nos besoins en analyse JPEG2000 DCI. Certains markers et métadonnées ne sont pas (encore) analysés. Vous aurez donc beaucoup moins de métadonnées pour vos images JPEG2000 DCI.

Références

SMPTE

ISO

Autres

Bibliographie

Dans ce paragraphe, j'ai indexé toutes les documentations que j'ai pu lire ou qui se trouvait dans mon historique de recherche. Il y a des documentations qui ne m'ont pas forcément servie, des liens que j'avais gardé au cas où, ou même des papiers qui ne correspondaient pas forcément aux recherches (en restant dans le thème JPEG2000/Wavelet). Plutôt que de faire un tri au risque d'écarter une ressource potentiellement intéressante, j'ai préféré toutes les annexer ici-même afin de ne léser aucun des auteurs ni leurs connaissances.

Notes

  1. Also, adjacent code-blocks from any given subband have overlapping regions of influence in the reconstructed image. This is because wavelet synthesis is a spatially expansive operation. This property tends to blur the boundaries between code-blocks in the reconstructed image, avoiding the appearance of hard boundary artifacts when individual block bitstreams are aggressively truncated. -- JPEG2000 Standard for Interactive Imaging (Taubman) ↩

  2. Il existe même d'autres résolutions. ↩

  3. The ability to enhance the quality associated with selected spatial regions in selected "quality layers" -- JPEG2000 Standard for Interactive Imaging (Taubman, Marcellin) et I only want to look at this area (...) I can build up the high for that and not waste pipeline bandwidth on the rest. -- Conférence de Ingrid Daubechies sur le ondelettes. ↩

  4. Certaines documentations, thèses, whitepapers utilisent plusieurs méthodes pour calculer le coefficient de détails comme : ↩

    • valeur moyenne moins la valeur secondaire du couple de valeurs - ou inversement : ( Approx - B )

    • valeur primaire moins valeur secondaire divisé par deux : ( A - B ) / 2

    • valeur moyenne moins la valeur primaire du couple de valeurs - ou inversement : ( Approx - A )

    • valeur minimale moins la valeur primaire du couple de valeurs - ou inversement : ( A - B )

    • valeur primaire moins la valeur secondaire : ( B - A )

    • valeur secondaire moins la valeur secondaire divisé par deux : ( B - A ) / 2

    Dans nos exemples, nous prendrons que la première solution et deuxième solution (les deux équations étant égales) car elles sont également utilisées comme référence de calcul pour les coefficients de détails dans la librairie pywt.

  5. C. Lifting and Reversibility, sch. Lifting steps for subband analysis -- JPEG2000: Standard for Interactive Imaging ↩

  6. Certaines documentations évoquent une valeur de 1.230174104914001 et 0.812893066. [1, 2, 3, 4] ↩

  7. Ce passage sur la conversion colorimétrique dans le JPEG2000 est assez confus dans l'ensemble des documentations : ↩

    • Ces deux citations indiquent que nous avons une conversion venant du XYZ en appliquant la matrice RGB → YCbCr :

    - In JPEG2000 lossy encoding, the forward ICT is applied to image components samples X, Y, Z as follows and generate the other three components such as YCz and Cx : Y = 0.299 X + 0.587 Y + 0.114 Z; Cz = -0.16875 X -0.33126 Y + 0.5 Z; Cx = 0.5 X -0.41869 Y -0.08131 Z -- Efficient lossless to lossy Transcoding of JPEG 2000 Codestreams for D-Cinema - These first three components can be interpreted as three color planes (R,G,B) for ease of understanding. That’s why they are often called multicomponent color transformation as well. However, they do not necessarily represent Red-Green-Blue data of a color image. -- JPEG2000 Standard for Image Compression Concepts

    • Tandis que d'autres évoquent un input devant être en RGB : Both of these transforms essentially map image data from the RGB to YCrCb color space. The transforms are defined to operate on the first three components of an image, with the assumption that components 0, 1, and 2 correspond to the red, green, and blue color planes. -- Coding of Still Pictures

    • Nous pouvons citer ce passage qui indique que l'input de la transformation étant du X'Y'Z', la sortie ne peut être considérée comme du YCbCr : The profiles require the use of the irreversible color transform (ICT). Note that the ICT is the wellknown RGB to YCbCr transform. However, in this case, the input color space is X’Y’Z’. Thus, the transformed components do not correspond to Y, Cb, and Cr -- JPEG2000 For Cinema

    • Enfin, nous pouvons également citer ce passage de la norme The ICT shall be used only with the 9-7 irreversible filter. The ICT is a decorrelating transformation applied to the first three components of an image (indexed as 0, 1 and 2). The three components input into the ICT shall have the same separation on the reference grid and the same bit-depth. -- JPEG2000 image coding system: Core coding system (ISO T.800 2015), accompagné de la matrice de conversion ci-dessous. On notera une note If the first three components are Red, Green and Blue components, then the Forward ICT is of a YCbCr transformation. qui fait écho à la citation juste au dessus.

    En conclusion, si nous prenons l'ensemble des citations, nous pouvons en conclure qu'avec notre X'Y'Z', nous devons appliquer quand même la conversion colorimétrique en utilisant la matrice nommée « RGB → YCbCr », mais qui ne sera ni un input RGB et ni un output YCbCr.

    À noter également les différences mineures dans la matrice de conversion entre deux grandes références sur le JPEG2000 :

    Dans JPEG2000 image coding system: Core coding system (ISO T.800 2015) et JPEG2000 Still Image Compression Standard, la matrice de conversion ICT est :

    Forward ICT :
0.299        0.587        0.114
-0.16875     -0.331260     0.5
0.5         -0.41869     -0.08131
------------------------------------
Reverse ICT :
1.0          0            1.402
1.0         -0.34413     -0.71414
1.0         -1.772        0

    Dans le livre JPEG2000 Standard for Image Compression Concepts, la matrice de conversion ICT est :

    Forward ICT :
0.299000     0.587000     0.114000
-0.168736    -0.331264     0.500000
0.500000    -0.418688    -0.081312
------------------------------------
Reverse ICT :
1.0          0.0          1.40210
1.0         −0.34414     −0.71414
1.0         −1.77180      0.0
          ---- ou ----
1.0          0.0          1.402000
1.0         −0.344136    −0.714136
1.0         −1.772000     0.0

  8. Voir note ci-dessus ↩

  9. JPEG2000 defines the division of each resolution level in rectangular regions called precincts. -- Model-Based JPEG2000 Rate Control Methods (Francesc Auli Llinàs) ↩

  10. Decomposition Level < Resolution Level: ↩

    • LL subband separate resolution level -- JPEG2000

    • Each resolution level consists of either the HL, LH, and HH subbands from one decomposition level or the NLLL subband. Thus, there is one more resolution level than there are decomposition levels -- JPEG2000

  11. The structure of a JPEG 2000 codestream is essentially key-length-value -- SMPTE 422:2019 - Mapping JPEG2000 Codestreams into the MXF Generic Container ↩

  12. The SOP and EPH marker segments shall not be present -- Legacy Compatibility Note 1 ↩

  13. Voir note ci-dessus  ↩

  14. The length of the main header plus the length of any of the tile-part headers shall be less than 255 bytes -- Legacy Compatibility Note 1 ↩

  15. 250 Mbits/sec total and a maximum of 200 Mbits/sec for the 2K portion of each color component. 24 FPS, a 2K distribution shall have a maximum of 1,302,083 bytes per frame (aggregate of all three color components including headers) (maximum of 1,041,666 bytes per color component per frame). 48 FPS, a 2K distribution shall have a maximum of 651,041 bytes per frame (maximum of 520,833 bytes per color component per frame ). 4K distribution shall have a maximum of 1,302,083 bytes per frame (aggregate of all three color components including headers) maximum of 250 Mbits/sec total and a maximum of 200 Mbits/sec for the 2K portion of each color component. -- DCI specifications ↩

  16. ( 250 / 24 = 10.41666 ) → 1.041.666 octets ↩

  17. ( 250 / 48 = 5.208333 ) → 520.833 octets ↩

  18. Compression - Bitrate : The maximum compressed bit rate for support of all proposed frame rates should be 500 Mb/sec. -- DCI High Frame Rates Digital Cinema Recommended Practice (2015), et The overall bit-rate is constrained to 500 Mb/s, the luminance channel (component 0) is constrained to 400 Mb/s and the combined data rates of the chrominance channels are constrained to 180 Mb/s. -- Kakadu JPEG2000 documentation ↩