Cryptographie : L'algorithme symétrique AES-CBC

Nous devons faire une petite excursion dans le monde magique de la cryptographie et comprendre ce qu'il se cache derrière l'acronyme AES et CBC.

Le chiffrement AES est un chiffrement dit chiffrement par bloc, c'est-à-dire qu'il va découper l'ensemble de votre message non-chiffré (surnommé plaintext ou en clair) en petit morceau de plusieurs octets tous de la même taille appelés blocs. Chaque bloc va être chiffré un par un puis ajouté à l'ensemble du corps chiffré (surnommé ciphertext ou cryptogramme)

Le mode CBC est un mode d'opération particulier ajouté lors du chiffrement AES pour améliorer le chiffrement, et que nous verrons plus en détail en dessous.

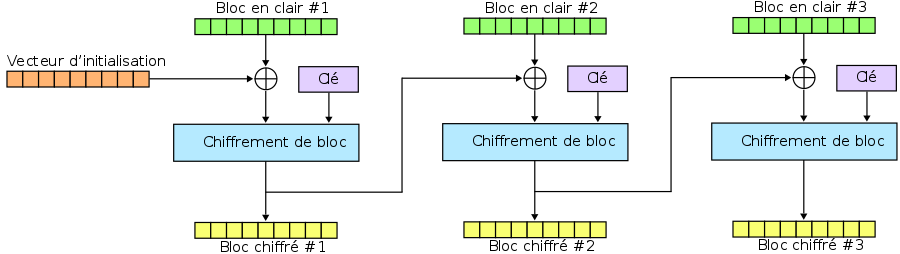
Préambule pour des raisons de facilité et de simplicité, dans nos exemples, chaque octet sera représenté par un caractère unique - au lieu de deux au format hexadécimal - et la clef de chiffrement sera entièrement à zéro - ce qui est une hérésie, je sais.

Un rapide résumé que nous allons voir dans ce chapitre à l'aide de ce schéma d'un encodage via AES-CBC :

Les différentes étapes d'un chiffrement AES-CBC

Nous allons voir concrètement comment se déroule un chiffrement à l'aide de l'algorithme de chiffrement AES et de son mode d'opération CBC.

Prenons un exemple concret avec un élément de 64 octets non-chiffrés : 

0123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0123456789ABCDEF

Dans notre cas du AES-128-CBC, chaque bloc sera de 16 octets - soit 128 bits :

0123456789ABCDEF 0123456789ABCDEF 0123456789ABCDEF 0123456789ABCDEF

Schématiquement avec la cryptographie AES-CBC, nous allons faire ceci :

En violet, nos deux passes cryptographiques :

CBC puis AES ? Cela peut sembler contre intuitif, mais pour un chiffrement, c'est d'abord le mode d'opération CBC qui s'applique puis AES. Lors d'un déchiffrement, cela sera effectivement AES puis CBC :)

La combinaison des deux donnent un chiffrement AES-CBC, et le fait de manipuler tous les éléments par des blocs de 16 octets (128 bits) donne le principe et le nom complet de AES-128-CBC.

Nous allons voir tout ceci en détail en commençant par Cipher Block Chaining (CBC) :

À l'intérieur du CBC

Une première passe va s'appliquer sur nos données avec le mode d'opération CBC.

Avec le principe du CBC, chaque nouveau bloc en clair va être chiffré en utilisant l'opérateur logique Ou-Exclusif surnommé "XOR".

Le XOR (symbolisé par ⊕) est assez simple et est beaucoup utilisé en cryptographie car il permet d'effectuer un chiffrement rapide et sûr avec un des principaux opérateurs informatiques (ET / OU / NON / NON-ET / NON-OU / XOR / NON-XOR):

Bit 1 Bit 2 Résultat
0 0 0
0 1 1
1 0 1
1 1 0

Pour résumer le fonctionnement de XOR : Quand les deux bits sont différents, alors le bit de résultat est 1.

Nous allons faire un exemple de chiffrement basique en XOR avec une lettre (donc 1 octet seulement) :

Convertissons nos lettres T et C directement en binaire :

Lettre Binaire Bit 1 Bit 2 Bit 3 Bit 4 Bit 5 Bit 6 Bit 7 Bit 8
T 01010100 0 1 0 1 0 1 0 0
C 01000011 0 1 0 0 0 0 1 1

Si nous appliquons un XOR pour chaque bit :

Lettre Binaire Bit 1 Bit 2 Bit 3 Bit 4 Bit 5 Bit 6 Bit 7 Bit 8
T 01010100 0 1 0 1 0 1 0 0
C 01000011 0 1 0 0 0 0 1 1
Calcul XOR 0 ⊕ 0 1 ⊕ 1 0 ⊕ 0 1 ⊕ 0 0 ⊕ 0 1 ⊕ 0 0 ⊕ 1 0 ⊕ 1
Résultat du XOR 0 0 0 1 0 1 1 1

Notre chiffrement donnera 00010111 (0x17 en hexadécimal).

L'avantage avec la simplicité du XOR, c'est qu'en prenant notre résultat (0x17) et en réappliquant notre clef C, nous retomberons sur notre lettre T. C'est la beauté de la simplicité de ce chiffrement symétrique pouvant être opéré même sur des circuits électroniques très basiques.

Appliquons maintenant ce principe avec notre bloc rouge de 16 octets.

0123456789ABCDEF 0123456789ABCDEF 0123456789ABCDEF 0123456789ABCDEF

Nous allons chiffrer le bloc en clair (A) 0123456789ABCDEF avec le précédent bloc bleu déjà chiffré dont le résultat AES-CBC donne 45A91E06B4CD871A et en utilisant la fonction XOR : Ceci nous donnera notre bloc rouge (B) :

Le fait d'utiliser le résultat chiffré du précédent bloc est le principe même du Cipher Block Chaining : chaque bloc chiffré sera dépendant de son prédécesseur (chaine), cela permet de renforcer la cryptographie car même en ayant les mêmes valeurs de départ dans les blocs en clair (01234456789ABCDEF) et avec la même clef de chiffrement AES (0000000000000000), chaque bloc chiffré sera totalement différent des autres au final.

Advanced Encryption Standard (AES)

Une seconde passe va s'appliquer sur nos données avec l'algorithme Advanced Encryption Standard (AES).

Maintenant que nous avons notre premier chiffrement, nous allons passer au chiffrement AES :

Notre bloc (B) va être une nouvelle fois chiffré mais cette fois à l'aide de l'algorithme AES :

Avec l'aide de la clef de chiffrement initiale (0000000000000000), l'algorithme AES va appliquer des transformations (Sub, Shift, Mix, ..) sur l'ensemble du bloc B :

A l'intérieur des transformations AES

Et cela plusieurs fois (10 tours pour du 128 bits), ce qui va produire un nouveau bloc chiffré (C) et qui sera notre résultat cryptographique final : Ce bloc, entièrement en AES-128-CBC, sera ajouté à l'ensemble de notre contenu chiffré.

Puis nous passons au bloc suivant avec le même principe. Le résultat du bloc C servira pour le XOR de notre bloc suivant, le bloc D, en vert, pour donner le bloc chiffré E. Puis il passera par l'algorithme AES avec la même clef pour arriver au bloc chiffré final F. Et on passera au bloc suivant, et ainsi de suite jusqu'à ce que tous les blocs soient chiffrés.

Ainsi, nous pouvons déjà dire que D22BAA265913B3B9C8D738B21B095846 (bloc C + bloc F) est une partie de notre contenu chiffré en AES-128-CBC (en enlevant toute rigueur cryptographique à notre démonstration ;-)

« Mais le premier bloc (bleu) n'a pas de bloc avant lui pour être utilisé lors du CBC du bloc n°1 ! »

Effectivement, pour le premier bloc, nous utilisons une petite astuce : le premier bloc sera chiffré (XOR) à l'aide d'un "faux précédent bloc" que nous aurons créé initialement nous-même et qui porte le nom de "IV" ou "Initialization Vector". C'est un bloc de 16 octets (128 bis) généré aléatoirement, il ne fait pas partie des données en clair, mais le résultat cryptographique fera partie du contenu chiffré (nous aurons besoin de cet IV lors du processus de déchiffrement)

Reprenons le schéma résumant ainsi ce que nous venons de voir :

Comme vous le voyez, tous les blocs s'enchaînent, sauf le premier qui utilise un vecteur d'initialisation (IV) pour son premier chiffrement.

Un exemple concret

Effectuons un chiffrement complet en AES-128-CBC avec notre programme fait-maison pour comprendre.

Pour la facilité, la taille de notre clef, de notre IV et de notre phrase secrète seront exactement de 16 octets (128 bits).

La clef cryptographique "UNE CLEF SECRETE" en hexadecimal :

    0x55 0x4E 0x45 0x20 0x43 0x4C 0x45 0x46
    0x20 0x53 0x45 0x43 0x52 0x45 0x54 0x45

Notre Initialization Vector (IV) en hexadécimal : 

    0x01 0x02 0x03 0x04 0x05 0x06 0x07 0x08
    0x09 0x10 0x11 0x12 0x13 0x14 0x15 0x16

Et enfin, notre phrase secrète "BONJOUR LE MONDE" en hexadécimal :

    0x42 0x4F 0x4E 0x4A 0x4F 0x55 0x52 0x20
    0x4C 0x45 0x20 0x4D 0x4F 0x4E 0x44 0x45

Le résultat chiffré donnera :

    0xEB 0x36 0xD4 0x79 0x25 0x6C 0x9E 0x6D
    0x1B 0xB4 0x11 0x52 0x6F 0x00 0x9C 0x1B

Et converti en texte :

    ë6Ôy%lžm´Roœ

Ce qui ne veut rien dire, et c'est le but :-)

Pour déchiffrer, on doit faire l'inverse :

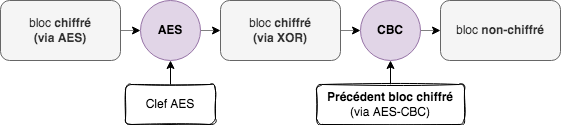
Tout d'abord, on déchiffre en AES le bloc, puis on le passe à CBC/XOR pour récupérer un bloc déchiffré, et ainsi de suite pour récupérer l'ensemble du texte non-chiffré.

En résumé

Pour chiffrer et déchiffrer un contenu en AES-128-CBC, il faudra :

A partir de cela, nous pouvons entrer dans le vif du sujet : La cryptographie appliquée à notre MXF.

Chapitres connexes

Références