Bitdepth 12 bits

Préface

Le passage à un bitdepth 12 bits est nécessaire pour finaliser le workflow. 1

Nous allons voir pourquoi ce choix et comment appliquer une conversion 12 bits.

Lexique

Dans la documentation, j'évoque des bits par composant, cela veut dire que chaque composant (par exemple le R du RGB, ou le X du XYZ) va avoir une certaine taille. Taille qui va permettre de stocker plus ou moins d'informations pour un seul composant !

Par exemple, si on dit "16 bits par composant" dans un RGB, cela voudra dire que la valeur rouge sera encodée en 16 bits, la valeur verte idem et la valeur bleue idem. En tout, pour faire une seule couleur (donc la fusion du R+G+B), cela va prendre 16+16+16 = 48 bits pour un seul pixel !

Il ne faudra pas confondre une couleur en 24 bits et un composant en 24 bits. Un composant en 24 bits, cela fait (R24+G24+B24) : un pixel de 72 bits au total. Une couleur en 24 bit représente donc les 3 composants directement, cela donne donc l'inverse : 24/3 = 8 bits par composant.

Autant dire que la différence entre la capacité de stockage d'un composant en 24 bits et une couleur encodé en 24 bits, il y a un énorme gap !

Dans toute la documentation et les normes SMPTE, nous ne parlons qu'en bits par composant.

Le choix du 12 bits

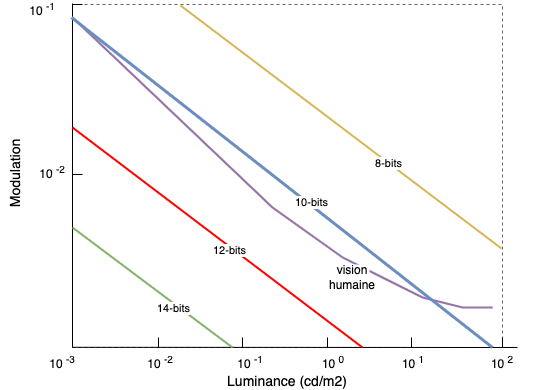
Le choix d'un bitdepth à 12 bits par composant se base sur le fait qu'avec 12 bits, l'oeil humain ne voit plus les différences et possibles artefacts. Nous aurions pu aller au-delà des 12 bits mais cela aurait nécessité plus de place de stockage pour un bénéfice inutile (pour la projection).

Ce choix 2 de 12 bits est lié au modèle Barten sur la sensibilité de contraste de l'oeil humain. Il a été étudié qu'en dessous de ~11 bits d'encodage (et d'autres paramètres), des artefacts peuvent être visibles suivant certaines conditions (par exemple, notre fameux banding déjà vu dans le chapitre Gamma). Au-delà, aucun artefact n'est visible.

Basé sur les données du livre Color and Mastering for Digital Cinema, voici un graphe complémentaire à celui au-dessus permettant de voir rapidement que la vision humaine tourne autour des 11 bits. En choisissant un bitdepth plus haut, on supprime tout potentiel problème :

Enfin, l'oeil humain peut distinguer au maximum environ 10 millions de couleurs. Avec un encodage en 12-bits, nous avons un échantillon de plus de 68 milliards de couleurs disponibles 3. Ça laisse un peu de marge...

Conversion de bitdepth

Le passage d'un bitdepth supérieur à 12 bits à un bitdepth à 12 bits nécessite la conversion des données et donc leurs destructions.

Par exemple, dans un bitdepth à 16 bits, nous avons la possibilité d'encoder une couleur (ou composante) sur 216 = 65.536 valeurs possibles pour une seule composant. En 12 bits, nous aurons 212 = 4096 valeurs possibles. Vous avez donc 16 fois moins de valeurs possibles. Il faut donc "recabler" les valeurs perdues du 16 bits dans les valeurs présentes du 12 bits.

Dans le cas d'une conversion réductive (downgrade), d'un 16 bits à un 12 bits, il faut d'abord voir l'intérieur du fichier d'origine car il existe une subtilité :

Images 16-bits venant d'un DCDM

Dans le cadre d'un DCDM 4, notre fichier TIF sera un faux 16 bits, il y aura 12 bits par composant mais stocké dans un "container" en 16 bits (12 bits pour le X stocké dans un 16 bits, pareil pour Y et Z), le reste des 4 bits de notre 12 bits sera un padding de zéro. C'est un choix établi par la norme SMPTE et les spécifications DCI pour avoir une conversion simple entre 16 bits et 12 bits. Dans ce cadre, il suffit juste de lire les 12 premiers bits et d'ignorer les 4 autres pour avoir nos 12 bits par composant sans destruction de données:

Exemple de la couleur blanche encodée en faux 16 bits:

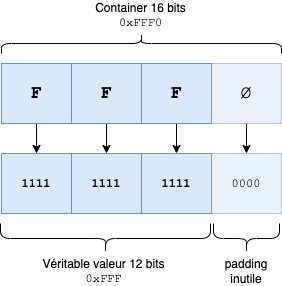
Si vous êtes dans ce cas de figure, vous n'avez (quasiment) rien à faire hormis de récupérer les 12 bits des 16 bits.

En C, il vous suffit de faire un décalage de 4 bits :

#include <stdio.h>
int main(void) {
    int a = 0xFFF0;
    printf("%x %d\n", a, a);
    printf("%x %d\n", a >> 4, a >> 4);
    return 0;
}

# gcc shift.c -o shift && ./shift
fff0 65520
fff 4095

En Python, c'est identique :

>>> a = 0xFFF0
>>> a >> 4
4095
>>> hex(a >> 4)
0xfff

Images 16 bits (ou plus) classiques

Sur un véritable 16 bits (ou supérieur) par composant, il faudra donc apporter une conversion colorimétrique pour ajuster la valeur 16 bits à une valeur 12 bits proche. Par exemple, en 16 bits, on passe de 281.474.976.710.656 valeurs possibles à 68.719.476.736 valeurs possibles en 12 bits, soit 4096 fois moins de possibilité. La valeur que nous aurons en 16 bits peut ne plus exister en 12 bits (et cela sera même la règle), il faudra donc "repositionner" la valeur dans le nouvel espace colorimétrique. On peut, par exemple, appliquer une table de correspondance (LUT) - long et fastidieux - ou bien simplement utiliser la magie de la conversion plage [0..1]).

Les couleurs dans une conversion

Un exemple extrême d'une conversion 16 bits à ... 2 bits (soit 223 = 64 valeurs possibles):

Dans la roue colorimétrique du haut, vous avez 16 bits par composant, soit 2163 donc 281.474.976.710.656 valeurs possibles ... une "petite" variété de combinaison.... l'image est assez bien détaillée. Si on passe à une conversion 2 bits, nous n'aurons que 223 = 64 couleurs possibles. Ici, nous faisons un (faux) essai avec seulement 16 couleurs, nous perdons des nuances, il faut donc "recabler" les couleurs perdues dans la nouvelle roue colorimétrique :


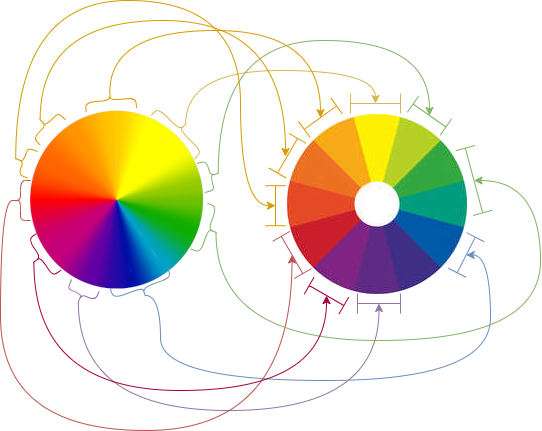
Par chance, il est possible de passer d'un bitdeph 16 bits (par exemple) à un bitdepth 12 bits avec un simple calcul que nous allons voir dans le prochain paragraphe.

Conversion technique de bitdepth

Petit rappel et comprendre les données que nous manipulons, notamment les valeurs binaires et hexadécimales de certaines bitdepth :

Valeurs maximales
Bitdepth Hexadecimal Binaire Décimal
8 bits 0xFF 1111.1111 255
12 bits 0xFFF 1111.1111.1111 4095
16 bits 0xFFFF 1111.1111.1111.1111 65.535
16 bits DCDM (*) 0xFFF0 1111.1111.1111.0000 65.520
(*) stockage d'un 12 bits dans un 16 bits. Les derniers bits ne sont donc pas utilisés.

La magie de la plage [0..1]

Pour convertir vers un bitdepth différent, il suffit en amont de convertir vos valeurs colorimétriques dans un range [0..1].

Une plage [0..1] est une plage où votre valeur minimale sera 0 (noir), votre valeur maximale sera à 1 (blanc) et votre valeur moyenne sera à 0.5 (gris). A partir de là, vos valeurs sont abstraites, vous pouvez travailler avec elles sans aucune limite.

Pour convertir votre valeur dans la plage [0..1], il vous suffit de la diviser par la valeur maximale de votre bitdepth d'origine. Pour convertir vers un autre bitdepth, il suffit de multiplier la valeur [0..1] par la valeur maximale de votre bitdepth de destination.

Par exemple, en 16 bits, vous diviserez par la valeur maximale en 16 bits qui est 0xFFFF :

# nouvelle_valeur = ancienne_valeur / 0xFFFF

>>> 0x0000/0xFFFF       # noir en 16 bits
0.0

>>> 0xFFFF/0xFFFF       # blanc en 16 bits
1.0

>>> 0x7FFF/0xFFFF       # gris en hexadecimal 16 bits
0.49999237048905165     # gris dans une plage [0..1]

L'avantage de cette conversion, c'est qu'à partir de là, vous pouvez convertir votre valeur 16 bits dans n'importe quel bitdepth.

Pour passer votre gris en 8 bits, il suffit de muliplier par la valeur maximale d'un 8 bits (255 valeurs maximum, donc 0xFF) :

>>> 0.49999237048905165 * 0xFF
127.49805447470817

127 sur 255 ... on est plutôt bon sur la valeur grise :)

A l'aide de la plage [0..1], vous pouvez convertir votre valeur relative dans n'importe quel bitdepth.

Conversion vers un nombre entier positif

Pour finaliser la conversion, on repasse tout en entier positif à l'aide d'une simple conversion de type (float → uint16 ou uint12) et nous rajoutons un petit round() 5 afin d'arrondir au chiffre le plus proche : 

# Avec la valeur 127.49
>>> int(127.49805447470817)
127
>>> int(round(127.49805447470817))
127

# Avec la valeur 127.51
>>> int(127.51)
127
>>> int(round(127.51))
128

# et enfin, passage en hexadécimal:
>>> hex(128)
'0x80'
# pour vérifier si c'est bien notre valeur du milieu :
>>> hex(int(round(0xFF / 2)))
'0x80'

Archivage / IMF

Le bitdepth est à 12 ou 16 bits.

Fichiers et Assets

Voici les différents fichiers, outils, codes et assets utilisés dans ce chapitre :

References

SMPTE :

Ressources :

Notes

  1. Le passage en 12 bits peut s'effectuer au début ou à la fin du workflow. L'avantage de le placer à la fin est que vous pouvez encore jouer dans un espace plus grand pendant les différentes conversions et avec une plus grande précision. ↩

  2. Archive: Contrast Sensitivity Experiment to Determine the Bit Depth for Digital Cinema ↩

  3. Dans la limite aussi (et surtout) de son espace colorimétrique. Si vous avez la possibilité de milliards de couleurs, vous pouvez être limité par son espace colorimétrique. Par exemple avec ces différents espaces colorimétriques par dessus nos couleurs visibles : 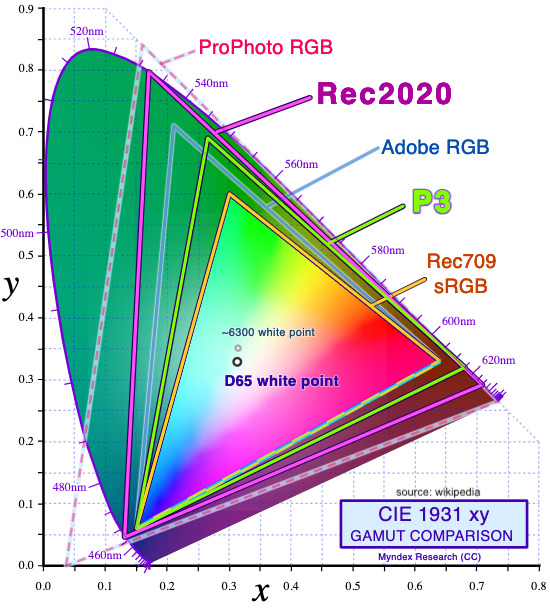Les différents "triangles" représentent nos différents espaces colorimétriques, et le "fer à cheval" est l'ensemble des couleurs disponibles. Vous constatez que certains espaces colorimétriques sont plus restreints que d'autres, et donc que certaines couleurs ne seront pas intégrées. Le bitdepth ne fait donc pas tout :-) ↩

  4. Voir SMPTE 428-1 - D-Cinema Distribution Master — Image Characteristics ↩

  5. C'est même une obligation d'effectuer cet arrondi : The INT operator returns the value of 0 for fractional parts in the range of 0 to 0.4999... and +1 for fractional parts in the range 0.5 to 0.9999..., i.e. it rounds up fractions above 0.5. -- SMPTE 428-1 - D-Cinema Distribution Master — Image Characteristics ↩