A gamma is a transition "method" between a linear world (such as computers) and a non-linear world (such as display or human vision). It is known as "Transfer Function" by the most knowledgeable and learned individuals.
Visually, a gamma involves adjusting the luminance. By manipulating the gamma, you can make an image either darker or brighter. These luminance changes are the result of gamma integration and the calculations below.
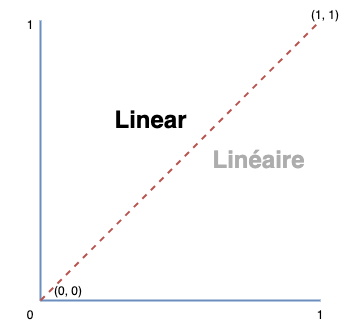
In a linear system, if we want to go from white to black, there will be a gradual and straight progression. For example, let's define that the black value as 0, the white as 1 and the gray as 0.5. We will have perfectly balanced intermediate steps which will form a perfectly straight line.

Each color will be equidistant from the previous and the next color :

In our example, with 10 values from absolute black to absolute white, each step increases by the same value (here, +10, but you can have another value).
For example, a camera operates using a linear system. Each photon is captured by a photosite on the sensor. If there is less light, the sensor converts fewer details. On the contrary, if there is more light, the sensor converts it with more details.
The human eye doesn't work the same way : An eye adapts to its environment and tries to counterbalance the lack of light, the darkness (low light, shadows) and the intense brightness (highlights). The eye is more sensitive to changes in luminosity than the changes in color. The eye can adjust the ambient lighting color to adapt certain color perceptions (such as white) in relation to its environment 1 : the eye perceives light non-uniformly, its response is non-linear.
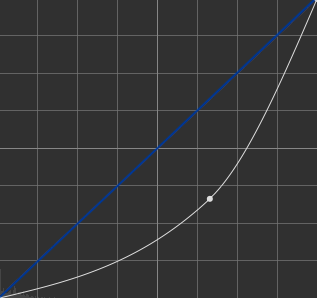
A non-linear system will produce a more or less distorted curve. Here an example with a gamma using a logarithm :
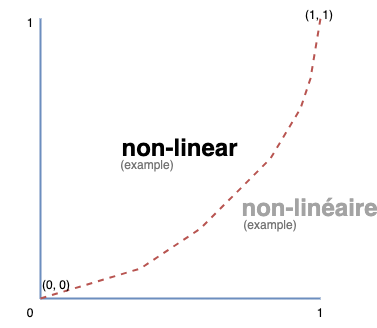
Thus, we will have this following form :

The transition from one value to another creates a certain curve.
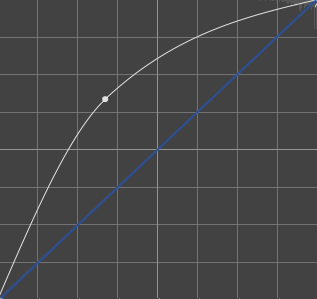
If we quickly compare both linear and non-linear example :


We observe that the whites are more white at the beginning and at the end; while blacks stay more to black.
A gamma allows an image to better match our real, non-linear visual perception. Thus, we apply a specific encoding on the image to better match its perception :
| Gamma lower than 1.0 | Gamma 1.0 (neutral) | Gamma upper than 1.0 |
|---|---|---|

|

|

|
|
|
|
A gamma curve will be more or less distorted depending on its value (2.2, 2.4, 2.6, ...)
We apply a gamma according to the viewing environment : the darker the room, the higher the gamma value. The brighter the room, the lower the gamma value :
So, why we use a gamma 2.6 ? Why not a gamma 2.8 or 3.0 ?
First, the theater is a very special place with a optimal environment compared to other environnment (such as office or your home, where the light can come from anywhere). The theater is a dark place without any stray light, allowing us to accentuate the contrast of the picture.
Another aspect is that a gamma of 2.6 closely matches human vision in this context of darkness. 3 :
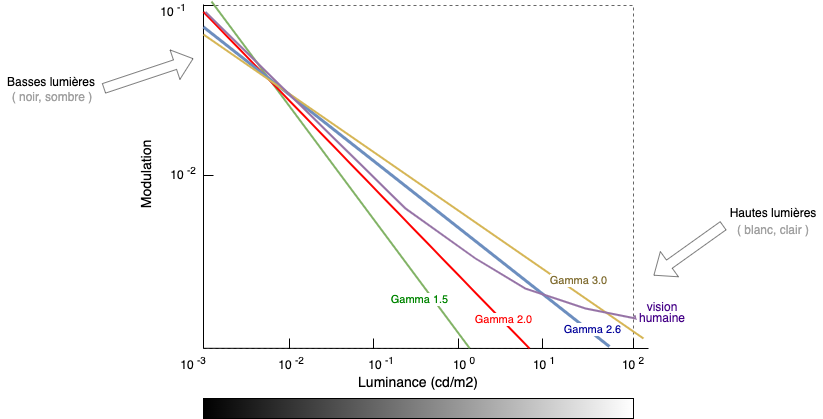
Based on the data from the book Color and Mastering for Digital Cinema, the diagram shows that the gamma of 2.6 is the most closely matches human vision.
In the top-left part, we have the low light (or shadows, dark). In the bottom-right part, the highlights (white, bright). You need to work with the different value levels in a way that stays below the threshold of human visual detection, while also avoiding unnecessary waste of values.
The purple curve matches the human vision. It should stay as much as possible below to avoid banding in the picture. Color banding happens when the transition from one color to another is too abrupt. These color bands may appear depending on the bitdepth chosen or the colorspace (gamut) used, and not just because of the wrong gamma. Most of the time, you can observe banding in the TV stream or on a DVD, particulary in the darkest areas of the picture. Here are some example with color banding from trailers :
It's important to understand that applying a gamma is mainly a technical choice: a gamma allows gradients (transition from one value to another) to be less visible to the human eye. Abrupt changes in value are more visible. A gamma curve allows values below the threshold of human vision (in purple).
Among all feasible gamma curves, gamma 2.6 is a good compromise.
Modifying gamma means either linearizing or delinearizing, both of which require a type of calculation based on the Power law using a gamma value of 2.6 as input (must be adapted according to the input) and 1/2.6 as output (DCI).
Don't forget the use of prime symbol ' means a gamma. Thus, a X'Y'Z' refers to a XYZ with a gamma. 4
Here are some examples of the gamma transformation from R'G'B' to X'Y'Z' and vice-versa :

From our R'G'B', we remove its 2.6 gamma curve (although it could also be a 2.2 gamma), it give us a linear RGB (1.0).
From there, we convert to XYZ, then we apply a 2.6 gamma (1/2.6) resulting in a XYZ with a gamma : X'Y'Z'
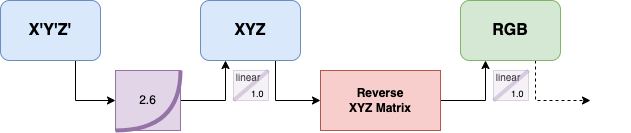
Here, it's the reverse, we start with an XYZ with gamma (X'Y'Z'), remove its 2.6 gamma (in blue), resulting in a linear XYZ (without gamma, or with a 1.0 gamma). After a reverse conversion, we obtain our RGB. From there, we can proceed with another conversion.
In the examples, we will work with 16-bit to be more precise.
In our document, we will use the pow() function to apply the power law in our calculations.
In mathematics, the pow() is a simple equation: f(x) = a.xg
The variable g represents our gamma value, which is either 2.6 or 1/2.6.
In Python - and in other languages - you can use the pow() function or the double-star :
>>> pow(1.5, 2.6)
2.8697051264080295
>>> (1.5**2.6)
2.8697051264080295
In C & C++, you can use the powf() function :
#include <stdio.h>
#include <math.h>
int main(void) {
float a = 1.5;
float g = 2.6;
printf("%.022f\n", powf(a, g));
return 0;
}
# gcc powfy.c -o powfy && ./powfy
2.8697049617767333984375
In the rest of the document, we will only use the pow() function to maintain consistency with several programming languages.
"Removing" a gamma means returning to a gamma of 1.0 :
| Gamma 0.38 (1 / 26) | Gamma 2.6 | Gamma 1.0 (neutral) | ||
|---|---|---|---|---|

|
+ |

|
= |

|
To make a gamma neutral, you just need to :
2.6 to a gamma 1/2.61/2.6 to a gamma 2.6From this point, we can see the different calculations in the following paragraphs.
It's a real dilemma. By default, they is no metadata that determines the gamma value (except if the file format allows including this type of metadata). Thus, we must determine it based on its colorspace.
| Level | Usage |
|---|---|
| 2.2 | sRGB, ... |
| 2.35 | Rec709 EBU Standard (rarely used) |
| 2.4 | Rec709 to compensate for high contrast on some display monitors, Rec2020 |
| 2.6 | DCI P3 |
Note that even if a standard exists for a type of colorspace and defines a specific gamma value (such as the sRGB gamma normalized to 2.2), you can have RGB with a gamma of 2.6 or even 2.0: the image creator might apply a more or less contrast for various reasons (even the craziest ones :)
Thus, be sure to verify wether the input gamma matches the standard-defined gamma.
Quick summary of the input and output DCI gammas before continuing :
1/2.61/2.6 by applying a gamma of 2.6. 2.6A gamma of 2.6 may be applied in two cases :
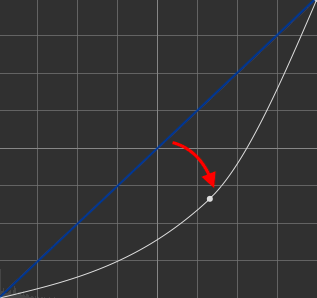
If you have a gamma of 1.0 (neutral), |
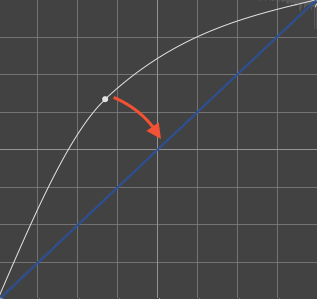
If you have a gamma of 1 / 2.6, |
To better understand the gamma conversion, here is the first example without a [0..1] range conversion and using the pow() function :
$ python3
r = pow(0xFFFF, 2.6) # 0xFFFF = decimal value of "65535"
3332963746773.969
g = pow(0xFFFF, 2.6)
3332963746773.969
b = pow(0xFFFF, 2.6)
3332963746773.969
In the white color, the red, the green and the blue are in maximal value, so 0xFFFF.
For our example, I'm using the hexadecimal value 0xFFFF because I'm used to working directly with the values that I can see in a hexadecimal viewer.
But it's better to work with decimal values - 65535 in our case.
Note that we are working with raw values (hexa or decimal): Using these kind of values may cause some issues: The floating-point values produced by pow() output are large, excessive and not useful in a mathematical workflow, and they may cause precision issues. That's why it's better to normalize all of these values to a safer base by using a [0..1] range. For reminder, putting a value into the [0..1] range means converting any decimal value into a value between 0.0 and 1.0.
Now, let's see an example with the [0..1] range conversion.
To do this, we divide your colorimetric value by its maximum value for the chosen bitdepth (here 16 bits, so 0xFFFF) :
$ python3
VALUE_MAX_16BITS = 0xFFFF # 65535
r = pow(0xFFFF / VALUE_MAX_16BITS, 2.6)
1.0
g = pow(0xFFFF / VALUE_MAX_16BITS, 2.6)
1.0
b = pow(0xFFFF / VALUE_MAX_16BITS, 2.6)
1.0
It's clearer with the [0..1] range : the minimum and maximum values produced by pow() will always be 0.0 (min) and 1.0 (max) respectively.
Note that with a 12-bit bitdepth, we will get (almost) the same result :
# 16-bit gamma conversion
>>> pow(0x7FFF / 0xFFFF, 2.6) # 0x7FFF = 32767 / 0xFFFF = 65535
0.16493194524645807
# 12-bit gamma conversion
>>> pow(0x7FF / 0xFFF, 2.6)
0.16483378645422764
The difference between 16-bit and 12-bit is totally normal, we don't have the same precision, so the power law will be different in the end. However, we observe that both results are 0.164.
Our first example without the [0..1] range conversion :
r = pow(0x1212, 2.6) # decimal value: 4626 (out of 65535)
3384812638.485899
g = pow(0x3434, 2.6) # decimal value: 13364 (out of 65535)
53386913590.93187
b = pow(0x5656, 2.6) # decimal value: 22102 (out of 65535)
197479534076.03644
Using the [0..1] range conversion :
VALUE_MAX_16BITS = 0xFFFF # 65535
r = pow(0x1212 / VALUE_MAX_16BITS, 2.6)
0.0010155563923436356
g = pow(0x3434 / VALUE_MAX_16BITS, 2.6)
0.016017850071908507
b = pow(0x5656 / VALUE_MAX_16BITS, 2.6)
0.05925042967154389
These values are linearized.
1/2.6A gamma of 1/2.6 may be applied in two cases :
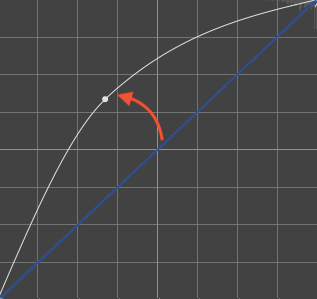
If you have a gamma of 1.0 (neutral), |
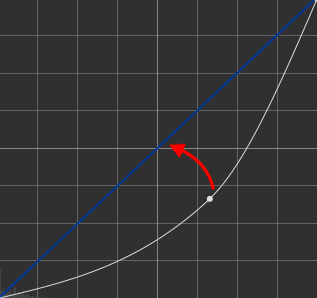
If you have a gamma of 2.6, |
1/2.6 conversionWe take the linearized values of white :
Without [0..1] range conversion :
r = pow(3332963746773.969, 1/2.6)
65534.99999999996
>>> hex(int(round(65534.99999999996)))
'0xffff'
g = pow(3332963746773.969, 1/2.6)
65534.99999999996
b = pow(3332963746773.969, 1/2.6)
65534.99999999996
With the white color, we observe that our output value is nearly the maximum possible value for 16-bit bitdepth (65535).
If we apply a round() and then hex(), the result is exactly 0xFFFF.
The same example using the [0..1] range conversion with the dark-blue color :
>> VALUE_MAX_16BITS = 0xFFFF # 65535
# (R)
>> pow(0.0010155563923436356, 1/2.6) * VALUE_MAX_16BITS
4626.000000000001
>>> hex(4626)
'0x1212'
# (G)
>> pow(0.016017850071908507, 1/2.6) * VALUE_MAX_16BITS
13364.000000000002
>>> hex(13364)
'0x3434'
# (B)
>> pow(0.05925042967154389, 1/2.6) * VALUE_MAX_16BITS
22102.0
>> hex(22102)
'0x5656'
The results are 0x1212, 0x3434 and 0x5656, just like before.
There are the differents files, tools, codes and assets used in this chapter :
Tools and codes :
Conversion: TIFF 16-bits to 8-bits : conversion_16bits-to-8bits.py
Conversion: TIFF 16-bits to 16-bits DCDM (12-bits into 16-bits) : conversion_16bits-to-16bits-DCDM.py
Conversion: RGB → XYZ (16-bits) (with Gamma) : conversion_rgb2xyz.py
Conversion: XYZ → RGB (16-bits) (with Gamma) : conversion_xyz2rgb.py
Conversion: RGB → XYZ (without Gamma) : conversion_rgb2xyz-without-gamma.py
Conversion: RGB → XYZ (without [0..1] range conversion) : conversion_rgb2xyz-without-conv-bitdepth.py
Tests out-of-bound : tests_out-of-bound.py
Tests conversions drifts : tests_drifts.py
Assets :
RGB 16-bits : rgb-16bits.tif
XYZ 16-bits : xyz-16bits.tif
XYZ 16-bits (without Gamma) : xyz-16bits-without-gamma.tif
RGB 8-bits : rgb-8bits.tif
XYZ 8-bits : xyz-8bits.tif
RGB 16-bits DCDM (12-bits into 16-bits) : rgb-16bits-DCDM.tif
Ressources :
Autres ressources :
This is precisely why, if you're standing outside a house and looking into a room, you might see warm colors (like yellow or orange). But once you go inside, after a short while, you’ll no longer perceive those warm tones as strongly - your eyes will have adapted. To learn more, see the article on visual adaptation ↩
References to the application of a 2.6 gamma in the transformation process : ↩
Color conversion from R’G’B’ to X’Y’Z’ requires a three-step process which involves linearizing the color-corrected R’G’B’ signals (by applying a 2.6 gamma function) -- SMPTE RP-431-2-2011 - DCinema Quality Reference Projector and Environement - Chapter « Color Conversion to XYZ »
The digital files were linearized (applying a gamma of 2.6), then a 3x3 matrix was applied to convert RGB to XYZ, followed by application of the 1 / 2.6 gamma function. The finished color-corrected files were stored as 12-bit X'Y'Z' data in 16-bit TIFF files. -- Color and Mastering for Digital Cinema (Glenn Kennel)
First, the R’G’B’ data is linearized by applying a simple gamma 2.6 transfer function : R = ( R / 4095 )2.6 -- SMPTE RP-431-2-2011 - DCinema Quality Reference Projector and Environment - Chapter « Color Conversion to XYZ »
And also to minimize the number of bits required for encoding, avoid contouring artifacts in image rendering, and achieve a better distribution of value levels within a limited encoding space (here, 12 bits). ↩
The X'Y'Z' notation show that the XYZ includes its transfer function which is - normally - only the gamma. However, in some documents, the white point normalization is included, and others suggest that the transfer function encompasses the entire equation int( 4095( L * X / 52.37 ) (1/2.6) ), thus combining the white point normalization, the gamma and the bitdepth. ↩