XYZ est un espace colorimétrique comme peut l'être le RGB. L'acronyme XYZ n'a aucune signification, contrairement à d'autres comme le RGB - contraction de Red, Green et Blue ou CMJN - contraction de Cyan, Magenta, Jaune et Noir.
Pourquoi le choix du XYZ ?
Pourquoi ne pas utiliser du RGB directement ?
Nous allons voir pourquoi dans ce chapitre.
Dans le chapitre histoire du cinéma numérique, j'avais évoqué le groupe SMPTE DC28 Color qui devait travailler sur tous les aspects colorimétriques. De longues (et houleuses ?) discussions sur le choix d'un espace colorimétrique, il a même été évoqué un "RGB Paramétrique" avec des métadonnées, mais a été écarté car si les métadonnées sont mal interprétées par le projecteur, les couleurs projetées seraient altérées.
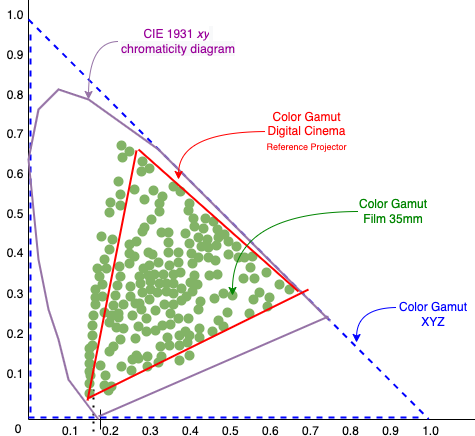
Au final, le groupe de recherche s'est tourné vers l'espace colorimétrique XYZ car il était le plus large, existe depuis des décennies (1931), était déjà utilisé dans pas mal de secteurs, était future-proof et englobait l'ensemble des couleurs (même en dehors du spectre visuel), il est tellement large qu'il peut intégrer l'espace colorimétrique de la projection cinéma numérique et celui du 35mm :

Il n'était pas dépendant de métadonnées ni du matériel de projection, sa luminance était encodée dans le Y, et enfin, son intégration dans les différents workflows n'aurait pas été si complexe que cela (il suffisait de linéariser le RGB, appliquer sa matrice de conversion 3x3 et d'encoder le gamma).
L'espace colorimétrique XYZ est tellement large (en bleu) qu'il peut intégrer l'ensemble du spectre visuel (en violet) et donc intégrer la quasi-totalité 1 des autres espaces colorimétriques. Nous pouvons donc passer vers un autre espace colorimétrique plus restreint sans trop de souci.
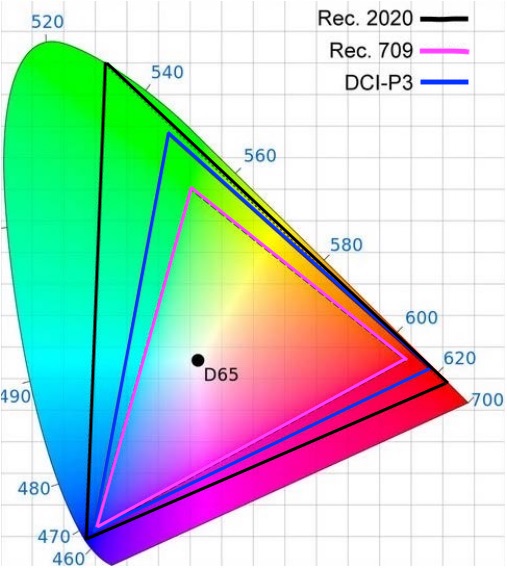
L'autre avantage est son indépendance à un autre espace colorimétrique. Alors que dans l'image, vous serez en XYZ, en sortie du projecteur, vous serez en DCI-P3 (voir chapitre « Espace colorimétrique DCI-P3 » ci-dessous). Le DCI-P3 est un espace colorimétrique plus large que le sRGB-Rec709 mais moins large que le Rec2020. Si un jour, les constructeurs de projecteurs décident de passer du DCI-P3 au Rec2020 (ou un DCI-P3-202x), il n'y aura aucun besoin de modifier l'encodage des images et donc des DCP. C'est l'avantage d'être en XYZ.
Pour en savoir plus à propos de l'histoire SMPTE du choix du XYZ, de leurs expériences dessus, et des équations mathématiques brutes, je vous conseille le livre Color and Mastering for Digital Cinema de Glenn Kennel qui consacre un chapitre entier sur tous ces aspects.
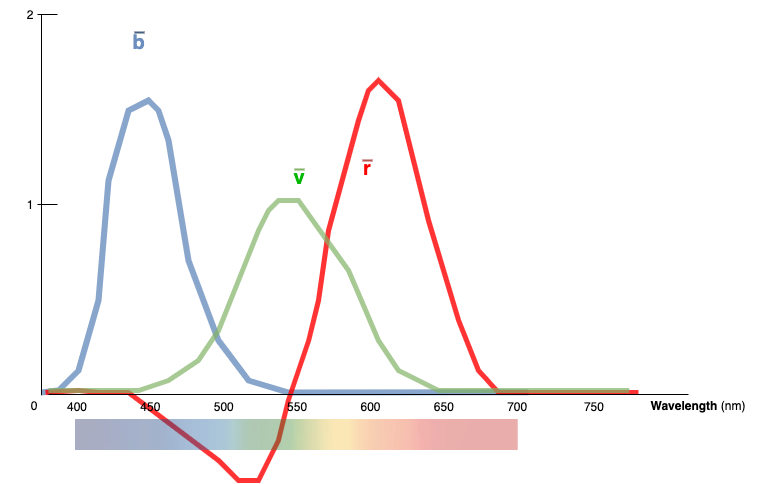
Dans les années 1920, afin de créer une définition stable d'un espace colorimétrique RGB, deux expérimentations sont lancées ... avec les moyens de l'époque : une poignée d' observateurs humains et des tests à l'oeil nu. Ces travaux vont amener à la publication d'un papier définissant les bases de ce que va être le CIE RGB :

Cependant, l'espace colorimétrique CIE RGB possède quelques soucis, notamment des valeurs négatives. Un exemple, le rouge étant par moment en dessous du zéro :
La Commission Internationale de l'Eclairage va lancer un nouvel espace colorimétrique dérivé du CIE RGB : le CIE XYZ. En 1931, l'espace colorimétrique XYZ est standardisé sous le nom de CIE XYZ 1931 :
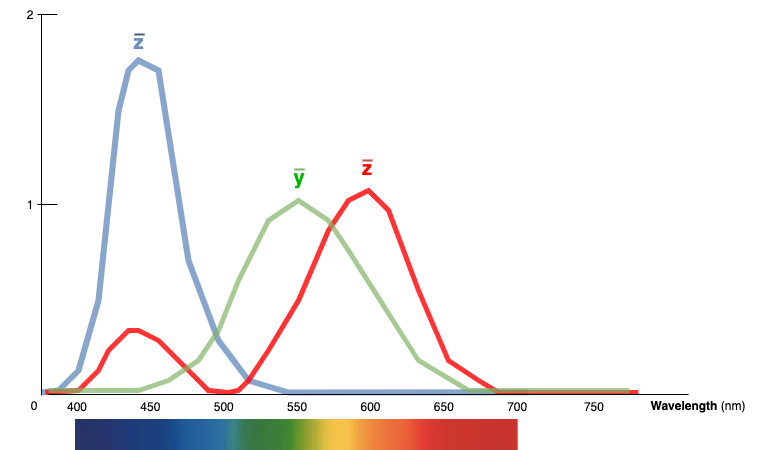
Pour nos courbes
Les primitives X, Y et Z n'ont pas de réalité physique 3, ce sont plus des concepts mathématiques, elles sont trois couleurs primaires fictionnelles (virtuelles) où le Y est le composant définissant la luminance, et où toutes les valeurs seront toujours positives 4, 5, 6.
Par la suite, il va exister des améliorations - de nouvelles "versions" - du XYZ à travers le temps : Pour éviter d'utiliser des moyens empiriques comme ceux de 1931 (un petit panel de personnes seulement et des instruments rudimentaires), les nouveaux XYZ proviennent maintenant de bases un peu plus solides et sont surnommés CIE XYZ 2006 et CIE XYZ 2015.
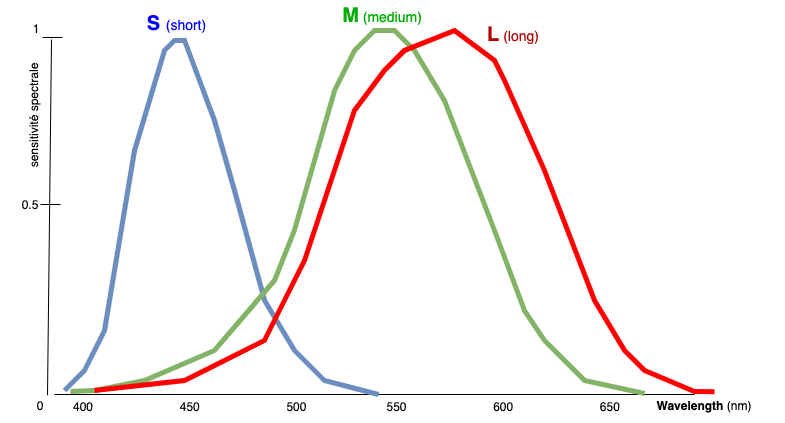
Par exemple, nous allons maintenant nous baser sur un espace colorimétrique LMS (pour Long, Medium et Short wavelengths), représentant l'absorption de la lumière par nos cônes dans la rétine de notre oeil. A l'aide d'expérimentation, nous arrivons à trois courbes représentées dans le schéma ci-dessous (LMS fonctions). À partir de nos différentes courbes LMS, nous pouvons alors générer les CIE XYZ Color Matching Functions (CMF) et ses différents
|
↔ |

|
| LMS fonctions | CIE XYZ Color Matching Functions |
Pour notre courbe LMS, les S, M et L représentent les différents cônes de réceptions visuels dans notre oeil. Ainsi, le S (bleu) va récupérer des couleurs bleues-violettes, Le M (vert) va récupérer les couleurs vertes, et le L (rouge) va récupérer des rouges-jaunes.
L'avantage est que depuis le LMS, nous pouvons générer un CIE RGB et un CIE XYZ avec de simples transformations linéaires à l'aide de matrices :
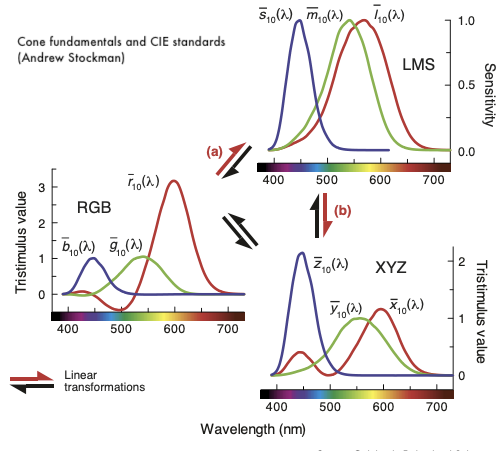
Un exemple avec une matrice de conversion de LMS vers XYZ 2006;2015 (noté
x = ( 1.94735469 -1.41445123 0.36476327 ) * ( l )
y = ( 0.68990272 0.34832189 0 ) * ( m )
z = ( 0 0 1.93485343 ) * ( s )
Ces dernières différentes fonctions et matrices sont des évolutions du CIE XYZ 1931 d'origine.
Cependant, le XYZ utilisé dans les DCP reste - pour l'instant - le CIE XYZ 1931. Dans un futur, avec les changements des différents workflows, il se peut que nous puissions passer à un CIE XYZ 2005;2016.
Si vous voulez en savoir plus sur l'histoire du XYZ, vous pouvez également vous reporter à ces deux sites :
Un petit aparté sur l'espace colorimétrique DCI-P3 que vous verrez de temps à autre dans ce chapitre.
Le RGB DCI-P3 est un espace colorimétrique plus large que sRGB / Rec709 (mais moins large que le nouveau Rec2020)
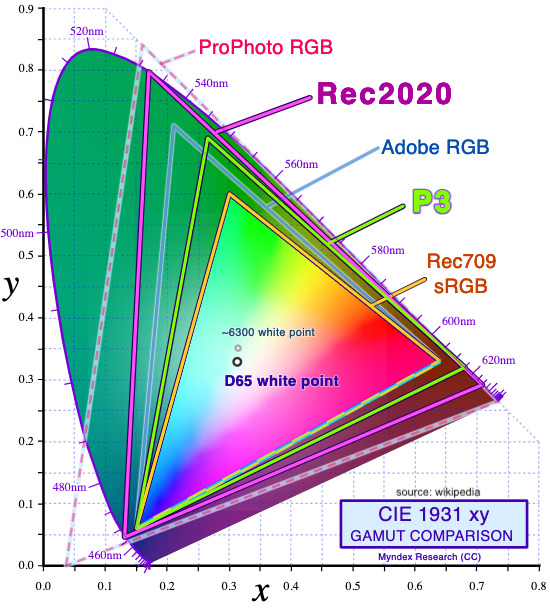
Le DCI-P3 est utilisé pour la projection en salle et aussi pour les sorties des logiciels d'étalonnages.
Petit récapitulatif :
Le DCI-P3 est un petit nom d'un RGB spécifique à la projection ou au workflow postproduction cinéma numérique.
Le DCI-P3 est la colorimétrie utilisée en projection et dans les sorties de logiciels d'étalonnages.
Les outputs en RGB DCI-P3 est avec un Gamma 2.6 [SMPTE-431-2]
Selon la source de votre input, vous serez amené à travailler sur plusieurs espaces colorimétriques comme du sRGB et/ou du RGB DCI-P3. Si vous avez des fichiers estampillés RGB, il faudra donc bien faire attention et distinguer ceux utilisant du sRGB et ceux utilisant du RGB DCI-P3. Conseil d'une personne qui a perdu parfois beaucoup de temps sur un sRGB pensant être du DCI-P3 ;-)
Si vous confondez les deux, les conversions ne seront pas les mêmes, les matrices seront différentes et les Gammas d'entrée aussi (un sRGB sera à 2.2 alors qu'un DCI-P3 sera à 2.6)
Les matrices de conversion XYZ utilisées dans les exemples du chapitre seront celles pour du RGB DCI-P3.
C'est ce format que vous verrez probablement le plus souvent en sortie de logiciels de postproduction.
Pour passer vers un XYZ, nous devons convertir chaque valeur de la source en appliquant un calcul matriciel sur ces dernières :

Derrière ces symboles se cachent une simple série d'additions et de multiplications entre la matrice NPM "RGB-to-XYZ" et la source (ici, RGB).
Le NPM (normalized primary matrix) est un simple "synonyme" pour préciser qu'on aura affaire à une matrice qui sera interchangeable selon la source en input.
Ainsi, si vous avez un input sRGB, vous aurez une matrice avec des chiffres spécifiques permettant de convertir le sRGB vers XYZ (ou inversement). Si vous avez un input DCI-P3, vous aurez une autre matrice, et ainsi de suite pour tous les autres espaces colorimétriques.
Ce normalized primary matrix est une matrice 3x3 8 qui va être multipliée par les valeurs en input pour donner son output XYZ :
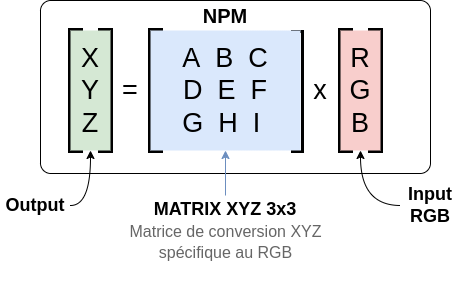
Ce calcul sous sa forme simplifiée (presque) :
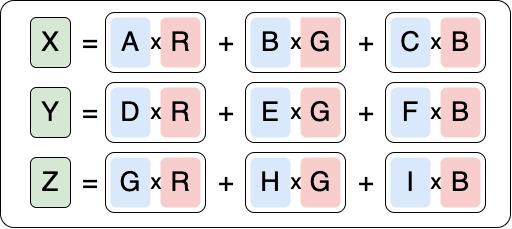
Ainsi, si par exemple, nous avons une matrice (NPM) XYZ de la sorte :
[ 1, 3, 4 ]
[ 6, 1, 2 ]
[ 8, 9, 5 ]
et un input :
[ 22, 33, 44 ]
Notre calcul matriciel sera :
( 1 * 22 ) + ( 3 * 33 ) + ( 4 * 44 )
( 6 * 22 ) + ( 1 * 33 ) + ( 2 * 44 )
( 8 * 22 ) + ( 9 * 33 ) + ( 5 * 44 )
A partir de là, nous pouvons appliquer n'importe quelle matrice pour n'importe quel input.
La conversion XYZ consiste donc à prendre chaque valeur de votre source et d'appliquer une matrice spécifique à son espace colorimétrique d'origine (sRGB, DCI-P3, ...) qui donnera des nouvelles valeurs pour son nouvel espace colorimétrique, XYZ.
Il existe plusieurs matrices de conversion vers XYZ (voir le chapitre Musée des matrices) car pour chaque espace colorimétrique d'origine, il existe autant de matrice de conversion, mais nous allons en prendre seulement deux, celle du RGB DCI-P3 et celle du sRGB/Rec709 [4matrix] :
La matrice officielle DCI-P3 → XYZ définie par le SMPTE 431-2 - Reference Projector and Environment :
| R x | G x | B x | ||||
|---|---|---|---|---|---|---|
| X | = | 0.4451698156 | + | 0.2771344092 | + | 0.1722826698 |
| Y | = | 0.2094916779 | + | 0.7215952542 | + | 0.0689130679 |
| Z | = | 0.0000000000 | + | 0.0470605601 | + | 0.9073553944 |
La matrice officielle sRGB/Rec709 → XYZ définie par la SMPTE RP-176 / RP-177 * :
| R | G | B | ||||
|---|---|---|---|---|---|---|
| X | = | 0.4123907993 | 0.3575843394 | 0.180487884 | ||
| Y | = | 0.2126390059 | 0.7151686788 | 0.0721923154 | ||
| Z | = | 0.0193308187 | 0.1191947798 | 0.9505321522 |
A partir d'une des matrices, nous avons effectué la conversion de chaque composant R,G,B en X,Y,Z:
X = (red * 0.4451698156) + (green * 0.2771344092) + (blue * 0.1722826698)
Y = (red * 0.2094916779) + (green * 0.7215952542) + (blue * 0.0689130679)
Z = (red * 0.0000000000) + (green * 0.0470605601) + (blue * 0.9073553944)
Notez qu'on suppose que votre input est linéarisé :
# Utilisation du bleu foncé :
# Rappel : Red (16 bits) = 0x1212
# Rappel : Green (16 bits) = 0x3434
# Rappel : Blue (16 bits) = 0x5656
red = 0.001016
green = 0.016018
blue = 0.059250
X = (red * 0.4451698156) + (green * 0.2771344092) + (blue * 0.1722826698)
Y = (red * 0.2094916779) + (green * 0.7215952542) + (blue * 0.0689130679)
Z = (red * 0.0000000000) + (green * 0.0470605601) + (blue * 0.9073553944)
>>> print(X, Y, Z)
0.0150991796848652 0.015854455599597 0.0545146231698818
Et voila ! vous avez votre première conversion vers XYZ.
Oui, c'est possible :)
convert "rgbp3_gamma26.tif" \
-gamma ".38461538461538461538" \ # linearize (1/2.6)
-color-matrix \ # conversion DCI-P3 -> XYZ
"0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.0000000000 0.0470605601 0.9073553944" \
-gamma "2.6" \ # delinearize
"export.tif"
En première ligne, on va linéariser (on enlève son Gamma 2.6 via son inverse 1/2.6), puis on applique la matrice de conversion DCI-P3 -> XYZ, puis on délinéarise de nouveau en rajoutant son petit Gamma 2.6
Notez que le programme n'est pas complet, nous n'appliquons ici qu'une conversion XYZ (et un gamma), il nous reste des étapes dans le workflow. Vous retrouverez un programme complet à cette adresse.
Si vous vous souvenez de notre schéma, il nous reste quelques étapes après notre conversion XYZ :

Pour finaliser, nous devons :
Vous pouvez passer dans les différents chapitres pour compléter votre connaissance. Ci-dessous, un résumé rapide des autres étapes :
A partir de notre dernière sortie XYZ, il vous suffit d'appliquer un petit gamma :
X = pow(X, 1/2.6)
Y = pow(Y, 1/2.6)
Z = pow(Z, 1/2.6)
>>> print(X, Y, Z)
0.19934137226195742 0.20311898286700303 0.326620520884937
Et enfin, on sort de notre plage [0..1] en repassant en 16 bits :
X = (X * 0xFFFF)
Y = (Y * 0xFFFF)
Z = (Z * 0xFFFF)
>>> print(X, Y, Z)
13063.83683118738 13311.402542189044 21405.075836194344
Comme vous voyez, nous avons des nombres décimaux. Cela va nous poser quelques soucis car le nombre 13063.83683118738 donne en hexadécimal 0x464c1f59 qui est en 32 bits... on est donc loin de nos 16 ou de nos 12 bits nécessaires :)
Le seul moyen est simplement de convertir ce nombre décimal (13063.83683118738) en nombre entier (13063 ou 13064).
On repasse tout en entier positif à l'aide d'une simple conversion de type (float → uint16 ou uint12) :
X = int(round(X))
Y = int(round(Y))
Z = int(round(Z))
>>> print(X, Y, Z)
13064 13311 21405
>>> print(hex(X), hex(Y), hex(Z))
0x3308 0x33ff 0x539d /* valeurs 16 bits */
Voici nos valeurs pour un X'Y'Z' 9 que nous pouvons inscrire dans notre fichier TIF 16 bits.
Si nous avions voulu passer en 12 bits, nous aurions appliquer ce calcul lors de la sortie de plage [0...1] :
X = (X * 0xFFF) /* 4095 */
Y = (Y * 0xFFF) /* 4095 */
Z = (Z * 0xFFF) /* 4095 */
>>> print(X, Y, Z)
816.3029194127156 831.7722348403775 1337.511033023817
X = int(round(X))
Y = int(round(Y))
Z = int(round(Z))
>>> print(hex(X), hex(Y), hex(Z))
0x330 0x340 0x53a /* valeurs 12 bits */
Nos valeurs sont bien en 12 bits, nous pouvons les inscrire dans notre fichier TIF 12 bits.
La matrice XYZ → DCI-P3 officielle définie par le SMPTE 432-1 - Color Processing for D-Cinema est la suivante :
| X * | Y * | Z * | ||||
|---|---|---|---|---|---|---|
| R | = | 2.7253940305 | + | -1.0180030062 | + | -0.4401631952 |
| G | = | -0.7951680258 | + | 1.6897320548 | + | 0.0226471906 |
| B | = | 0.0412418914 | + | -0.0876390192 | + | 1.1009293786 |
La matrice officielle XYZ → sRGB/Rec709 définie par la SMPTE RP-176 :
| X * | Y * | Z * | ||||
|---|---|---|---|---|---|---|
| R | = | 3.2409699419 | + | -1.5373831776 | + | -0.4986107603 |
| G | = | -0.9692436363 | + | 1.8759675015 | + | 0.0415550574 |
| B | = | 0.0556300797 | + | -0.2039769589 | + | 1.0569715142 |
La matrice officielle XYZ → Rec2020 :
| X * | Y * | Z * | ||||
|---|---|---|---|---|---|---|
| R | = | 1.7166511880 | + | -0.3556707838 | + | -0.2533662814 |
| G | = | -0.6666843518 | + | 1.6164812366 | + | 0.0157685458 |
| B | = | 0.0176398574 | + | -0.0427706133 | + | 0.9421031212 |
A partir de cette matrice, nous avons effectuer la conversion de chaque composant X,Y,Z vers R,G,B :
# Utilisation du bleu foncé :
# Rappel : Red (16 bits) = 0x1212
# Rappel : Green (16 bits) = 0x3434
# Rappel : Blue (16 bits) = 0x5656
# Rappel : red = 0.001016
# Rappel : green = 0.016018
# Rappel : blue = 0.059250
X = 0.0150991796848652
Y = 0.015854455599597
Z = 0.0545146231698818
red = (X * 2.7253940305) + (Y * -1.0180030062) + (Z * -0.4401631952)
green = (X * -0.7951680258) + (Y * 1.6897320548) + (Z * 0.0226471906)
blue = (X * 0.0412418914) + (Y * -0.0876390192) + (Z * 1.1009293786)
print(red, green, blue)
0.0010159999969451862 0.01601799999824417 0.059250000001124806
Dû à l'imprécision de la matrice de décodage XYZ→RGB, nous arrivons sur des chiffres légèrement décalés par rapport à notre origine mais après conversion en 16 ou 12 bits, vous retrouverez vos petits :
# Conversion en 16 bits :
>>> print(
hex(int(0.0010159999969451862 * 0xFFFF)),
hex(int(0.01601799999824417 * 0xFFFF)),
hex(int(0.059250000001124806 * 0xFFFF))
)
0x42 0x419 0xf2a
# Comparaison avec nos références
>>> print(
hex(int(0.001016 * 0xFFFF)),
hex(int(0.016018 * 0xFFFF)),
hex(int(0.059250 * 0xFFFF))
)
0x42 0x419 0xf2a
Pour voir une dérivation, il faut arriver au-delà des 32 bits par composant (à l'aide de ce petit programme) :
RGB = 0.07058823529411765 0.20392156862745098 0.33725490196078434
XYZ = 0.14604061004705882 0.1851777539607843 0.31560671781803923
RGB = 0.07058823527801708 0.2039215686187231 0.337254901974168
8 bits : 0x12 0x34 0x56
8 bits : 0x12 0x34 0x56
10 bits : 0x48 0xd1 0x159
10 bits : 0x48 0xd1 0x159
12 bits : 0x121 0x343 0x565
12 bits : 0x121 0x343 0x565
16 bits : 0x1212 0x3434 0x5656
16 bits : 0x1212 0x3434 0x5656
20 bits : 0x12121 0x34343 0x56565
20 bits : 0x12121 0x34343 0x56565
24 bits : 0x121212 0x343434 0x565656
24 bits : 0x121212 0x343434 0x565656
28 bits : 0x1212121 0x3434343 0x5656565
28 bits : 0x1212121 0x3434343 0x5656565
30 bits : 0x4848484 0xd0d0d0d 0x15959595
30 bits : 0x4848484 0xd0d0d0d 0x15959595
32 bits : 0x12121212 0x34343434 0x56565656
32 bits : 0x12121212 0x34343434 0x56565656
34 bits : 0x48484848 0xd0d0d0d0 0x159595959
34 bits : 0x48484848 0xd0d0d0d1 0x159595959
# drift on 34 bits
36 bits : 0x121212120 0x343434342 0x565656566
36 bits : 0x121212121 0x343434343 0x565656565
# drift on 36 bits
40 bits : 0x1212121200 0x343434342a 0x5656565665
40 bits : 0x1212121212 0x3434343434 0x5656565656
# drift on 40 bits
48 bits : 0x12121212005e 0x343434342a9b 0x56565656650d
48 bits : 0x121212121212 0x343434343434 0x565656565656
# drift on 48 bits
56 bits : 0x12121212005e2a 0x343434342a9b86 0x56565656650d84
56 bits : 0x12121212121212 0x34343434343434 0x56565656565658
# drift on 56 bits
64 bits : 0x12121212005e2a00 0x343434342a9b8600 0x56565656650d8400
64 bits : 0x1212121212121200 0x3434343434343400 0x5656565656565800
# drift on 64 bits
On constate la dérive à partir de 34 bits, ce qui laisse un certain delta puisque nous n'irons qu'à 12 bits et si - dans un futur, on augmente, nous n'irons pas jusqu'au 32 bits.
Après un calcul de conversion XYZ inversée (donc pour revenir vers RGB, par exemple), il arrive que vos valeurs soient en out-of-bound, elles sont soient négatives, soient elles dépassent la limite maximale dans le bitdepth.
Par exemple, si votre valeur 16 bits est de 65536.370088, vous savez que vous ne pourrez pas stocker cette valeur dans un 16 bits car la valeur maximale dans un 16 bits est de 65535. Vous allez devoir redresser ces valeurs.
Pour cela, pas besoin de calculs compliqués, si vos valeurs sont négatives ou supérieures à la valeur maximale, cela veut dire que vous êtes soit sur un blanc total soit sur un noir total (soit « une couleur XYZ qui est en dehors de l'espace RGB choisi, surnommé "Out of Gamut" » 10 ) . Auquel cas, il suffit d'écraser l'ancienne valeur soit par un 0, soit par la valeur maximale de votre bitdepth.
Par exemple :
A cause de ces dérives, n'essayez pas - sauf dernier chance et cas extrême - de retrouver votre film en convertissant depuis votre XYZ. Préférez toujours garder un DCDM ou un des fichiers d'origine en 16 bits ou supérieur.
Même si la dérive est minime, vous perdrez de l'information, déjà de par la conversion en 12 bits.
Après, si vous n'avez plus le choix...
Voici les différentes matrices de références SMPTE.
# RGB DCI-P3 -> XYZ:
0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.2094916779 0.0470605601 0.9073553944
# XYZ -> RGB DCI-P3
2.7254 -1.0180 -0.4402
-0.7952 1.6897 0.0226
0.0412 -0.0876 1.1009
# RGB DCI-P3 -> XYZ
0.4453 0.2770 0.1724
0.2096 0.7216 0.0690
0.0001 0.0470 0.9082
# RGB DCI-P3 -> XYZ - Reference Projector
0.4452 0.2771 0.1723
0.2095 0.7216 0.0689
0.0000 0.0471 0.9074
# RGB DCI-P3 -> XYZ - Reference Projector 10 significant digits
0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.0000000000 0.0470605601 0.9073553944
# XYZ - RGB DCI-P3 - 10 significant digits
2.7253940305 -1.0180030062 -0.4401631952
-0.7951680258 1.6897320548 0.0226471906
0.0412418914 -0.0876390192 1.1009293786
# RGB DCI-P3 -> XYZ
0.4452 0.2771 0.1723
0.2095 0.7216 0.0689
0.0000 0.0471 0.9074
Voici les différentes matrices glanées dans les différentes documentations, livres ou sources. Notez que ces matrices peuvent inclure des corrections chromatiques dans leurs chiffres finaux.
# sRGB linear (D65) -> XYZ (Simple, 4 digits) [D65->D65]
X = 0.412453 0.357580 0.180423
Y = 0.212671 0.715160 0.072169
Z = 0.019334 0.119193 0.950227
# sRGB linear (D65) -> XYZ (Better, 5 digits)
X = 0.4124564 0.3575761 0.1804375
Y = 0.2126729 0.7151522 0.0721750
Z = 0.0193339 0.1191920 0.9503041
# SMPTE RP-177 / RP-176 / Glenn Kennel book
X = 0.4123907993 0.3575843394 0.1804807884
Y = 0.2126390059 0.7151686788 0.0721923154
Z = 0.0193308187 0.1191947798 0.9505321522
# XYZ -> RGB Rec709 (SMPTE RP177)
X = 0.4123907993 0.3575843394 0.1804807884
Y = 0.2126390059 0.7151686788 0.0721923154
Z = 0.0193308187 0.1191947798 0.9505321522
# DC28.30 (2006) - Proj Ref.
0.4451698156 0.2771344092 0.1722826698
0.2094916779 0.7215952542 0.0689130679
0.0000000000 0.0470605601 0.9073553944
# StEM
0.464, 0.2692, 0.1610, 0,
0.2185, 0.7010, 0.0805, 0,
0.0000, 0.0457, 0.9087, 0,
# from Journal SMPTE (October 2009)
| 0.41239080 0.3575843 0.18048079
REC709 -| 0.21263901 0.7151687 0.07219232
| 0.01933082 0.1191948 0.95053215
XYZ = ( 0.950456, 1.000000, 1.089058 )
# from SMPTE RP-431:
# R'G'B' (2.6) -> RGB [] -> XYZ (2.6) -> X'Y'Z'
X = 0.4451698156 0.2771344092 0.1722826698 -> Rdc
Y = 0.2094916779 0.7215952542 0.0689130679 -> Gdc
Z = 0.0000000000 0.0470605601 0.9073553944 -> Bdc
Rdc = 2.7254 -1.0180 -0.4402 -> X
Gdc = -0.7952 1.6897 0.0226 -> Y
Bdc = 0.0412 -0.0876 1.1009 -> Z
# ColorFAQ (https://poynton.ca/notes/colour_and_gamma/ColorFAQ.html)
X ( 0.412453, 0.357580, 0.180423 ) sR
Y ( 0.212671, 0.715160, 0.072169 ) sG
Z ( 0.019334, 0.119193, 0.950227 ) sB
# A Guided Tour of Color Space
# CIE XYZ -> Rec. 709 RGB (D65)
R709 = ( 3.240479, −1.537150, −0.498535 ) * X
G709 = ( −0.969256, 1.875992, 0.041556 ) * Y
B709 = ( 0.055648, −0.204043, 1.057311 ) * Z
------
X = ( 0.412453 0.357580 0.180423 ) * R709
Y = ( 0.212671 0.715160 0.072169 ) * G709
Z = ( 0.019334 0.119193 0.950227 ) * B709
# GammaFAQ (https://poynton.ca/notes/colour_and_gamma/GammaFAQ.html)
Y (luminance) = 0.2126 (R) + 0.7152 (G), 0.0722 (B) = 1.0
# SMPTE RP 177-1993 :
# Luminance Equation :
Y = 0.2126390059 (R) + 0.7151686788 (G) + 0.0721923154 (B) = 1.0
# DCI-HDR-D-Cinema-Addendum
# https://documents.dcimovies.com/HDR-Addendum/54a2b12fba306370323b0ec7de542ade91581047/#sec-C-2
X ( 0.4865709486482242 0.26566769316910 0.19821728523436 ) R
Y ( 0.22897456406975 0.69173852183651 0.07928691409375 ) G
Z ( 0 0.04511338185890 1.04394436890098 ) B
-------------------------------------------------------------------------
R ( 2.49349691194142 -0.93138361791914 -0.40271078445070 ) X
G ( −0.82948896956157 1.76266406031835 0.02362468584193 ) Y
B ( 0.03584583024378 −0.07617238926804 0.95688452400768 ) Z
-------------------------------------------------------------------------
# SMPTE Journal Nov/Dec 2014
# RGB (BT709) to XYZ
X = 0.4124 0.3576 0.1805 * R709
Y = 0.2126 0.7152 0.0722 * G709
Z = 0.0193 0.1192 0.9505 * B709
# XYZ to RGB (BT2020)
R2020 = 0.6370 0.1446 0.1689 * X
G2020 = 0.2627 0.6780 0.0593 * Y
B2020 = 0.0000 0.0281 1.0610 * Z
# Merged R2020->R709
R2020 = 0.6274 0.3293 0.0433 * R709
G2020 = 0.0691 0.9195 0.0114 * G709
B2020 = 0.0164 0.0880 0.8956 * B709
# XYZ->sRGB (FreeDCPPlayer)
sR = { 3.2404542, -1.5371385, -0.4985314 } * X
sG = { -0.9692660, 1.8760108, 0.0415560 } * Y
sB = { 0.0556434, -0.2040259, 1.0572252 } * Z
# XYZ->sRGB (image-engineering.de)
sR = 3.2410 -1.5374 -0.4986 * X
sG = -0.9692 1.8760 0.0416 * Y
sB = 0.0556 -0.2040 1.0570 * Z
# XYZ->sRGB (Franck Chopin)
R = 3.24045416 -0.96926603 0.05564343
G = -1.53713851 1.87601085 -0.20402591
B = -0.49853141 0.04155602 1.05722519
# XYZ->sRGB (RP177, François Helt, Franck Chopin)
R = 3.240575326758 -1.537195988334 -0.498550050270
G = -0.969283339828 1.876044347577 0.041556759645
B = 0.055627459197 -0.203967350390 1.056921724748
# Color and Mastering (Kennel)
X 0.4452 0.2771 0.1723 * R
Y 0.2095 0.7216 0.0689 * G
Z 0.0000 0.0471 0.9074 * B
---------------------------------------------
R 2.7254 -1.0180 -0.4402 * X
G -0.7952 1.6897 -0.0226 * Y
B 0.0412 -0.0876 1.1009 * Z
# SMPTE 432-1-2010 - Digital Source Processing - Color Processing D-Cinema
# Linear RGB -> Linear XYZ
X = 0.4361343357 0.3327206339 0.1888489579 R
Y = 0.2180671678 0.6941240810 0.0878087511 G
Z = 0.0167743975 0.1204678157 0.9262018955 B
# AMPAS Aces
# https://github.com/ampas/aces-dev/blob/v1.0.3/transforms/ctl/README-MATRIX)
# AP0-to-XYZ :
R_out = 0.9525523959 * R_in + 0.0000000000 * G_in + 0.0000936786 * B_in;
G_out = 0.3439664498 * R_in + 0.7281660966 * G_in + -0.0721325464 * B_in;
B_out = 0.0000000000 * R_in + 0.0000000000 * G_in + 1.0088251844 * B_in;
# XYZ-to-AP0 :
R_out = 1.0498110175 * R_in + 0.0000000000 * G_in + -0.0000974845 * B_in;
G_out = -0.4959030231 * R_in + 1.3733130458 * G_in + 0.0982400361 * B_in;
B_out = 0.0000000000 * R_in + 0.0000000000 * G_in + 0.9912520182 * B_in;
# AP1-to-XYZ :
R_out = 0.6624541811 * R_in + 0.1340042065 * G_in + 0.1561876870 * B_in;
G_out = 0.2722287168 * R_in + 0.6740817658 * G_in + 0.0536895174 * B_in;
B_out = -0.0055746495 * R_in + 0.0040607335 * G_in + 1.0103391003 * B_in;
# XYZ-to-AP1 :
R_out = 1.6410233797 * R_in + -0.3248032942 * G_in + -0.2364246952 * B_in;
G_out = -0.6636628587 * R_in + 1.6153315917 * G_in + 0.0167563477 * B_in;
B_out = 0.0117218943 * R_in + -0.0082844420 * G_in + 0.9883948585 * B_in;
# XYZ-to-P3D60 :
R_out = 2.4027414142 * R_in + -0.8974841639 * G_in + -0.3880533700 * B_in;
G_out = -0.8325796487 * R_in + 1.7692317536 * G_in + 0.0237127115 * B_in;
B_out = 0.0388233815 * R_in + -0.0824996856 * G_in + 1.0363685997 * B_in;
# P3D60-to-XYZ :
X_out = 0.5049495342 * R_in + 0.2646814889 * G_in + 0.1830150515 * B_in;
Y_out = 0.2376233102 * R_in + 0.6891706692 * G_in + 0.0732060206 * B_in;
Z_out = 0.0000000000 * R_in + 0.0449459132 * G_in + 0.9638792711 * B_in;
# XYZ-to-P3DCI:
R_out = 2.7253940305 * R_in + -1.0180030062 * G_in + -0.4401631952 * B_in;
G_out = -0.7951680258 * R_in + 1.6897320548 * G_in + 0.0226471906 * B_in;
B_out = 0.0412418914 * R_in + -0.0876390192 * G_in + 1.1009293786 * B_in;
# XYZ-to-REC709:
R_out = 3.2409699419 * R_in + -1.5373831776 * G_in + -0.4986107603 * B_in;
G_out = -0.9692436363 * R_in + 1.8759675015 * G_in + 0.0415550574 * B_in;
B_out = 0.0556300797 * R_in + -0.2039769589 * G_in + 1.0569715142 * B_in;
# XYZ-to-REC2020:
R_out = 1.7166511880 * R_in + -0.3556707838 * G_in + -0.2533662814 * B_in;
G_out = -0.6666843518 * R_in + 1.6164812366 * G_in + 0.0157685458 * B_in;
B_out = 0.0176398574 * R_in + -0.0427706133 * G_in + 0.9421031212 * B_in;
# XYZ -> RGB24
# ref : openjpeg/thirdparty/libtiff/tif_luv.c
R = 2.690*X + -1.276*Y + -0.414*Z
G = -1.022*X + 1.978*Y + 0.044*Z
B = 0.061*X + -0.224*Y + 1.163*Z
En complément, vous trouverez une masse importante de matrices Input→XYZ ou XYZ→Output compilées par Bruce Lindbloom dans son article RGB/XYZ Matrices. copie locale
Les inclassables (pour l'instant) :
(L étant à 48 cd/m2)
Vous pouvez vous amuser avec Python et Colour Science :
>>> import numpy as np
>>> import colour
>>> primaries_xyz = [0.64, 0.33, 0.3, 0.6, 0.15, 0.06]
>>> d65_illuminant = colour.CCS_ILLUMINANTS.get('CIE 1931 2 Degree Standard Observer').get('D65')
# array([ 0.3127, 0.329 ])
>>> np.linalg.inv(
colour.normalised_primary_matrix(
primaries_xyz,
d65_illuminant
)
)
array([
[ 3.24096994, -1.53738318, -0.49861076],
[-0.96924364, 1.8759675 , 0.04155506],
[ 0.05563008, -0.20397696, 1.05697151]
])
Le résultat correspond à la matrice officielle XYZ → sRGB/Rec709 définie par la SMPTE RP-176.
Vous pouvez retrouver aussi des conversions XYZ/RGB avec les méthodes sRGB_to_XYZ ou XYZ_to_sRGB
Voici les différents fichiers, outils, codes et assets utilisés dans ce chapitre :
Conversion TIFF 16-bits à 8-bits : conversion_16bits-to-8bits.py
Conversion TIFF 16-bits à 16-bits DCDM (12-bits dans du 16-bits) : conversion_16bits-to-16bits-DCDM.py
Conversion RGB → XYZ (16-bits) (avec Gamma) : conversion_rgb2xyz.py
Conversion XYZ → RGB (16-bits) (avec Gamma) : conversion_xyz2rgb.py
Conversion RGB → XYZ (sans Gamma) : conversion_rgb2xyz-without-gamma.py
Conversion RGB → XYZ (sans conversion plage [0..1]) : conversion_rgb2xyz-without-conv-bitdepth.py
Conversion complète RGB-DCI-P3 → X'Y'Z conforme DCI/SMPTE (16 bits) : conversion_dcip3_to_xyz.sh
Conversion complète DCI-P3 → X'Y'Z conforme DCI/SMPTE (16 bits) (Python) conversion_dcip3_to_xyz.py
Conversion complète DCI-P3 → X'Y'Z conforme DCI/SMPTE (16 bits) (ImageMagick) conversion_dcip3_to_xyz.sh
Conversion complète sRGB → X'Y'Z conforme DCI/SMPTE (16 bits) (Python) conversion_srgb_to_xyz.py
Conversion complète sRGB → X'Y'Z conforme DCI/SMPTE (16 bits) (ImageMagick) conversion_srgb_to_xyz.sh
Tests out-of-bound : tests_out-of-bound.py
Tests Dérivations de conversions : tests_drifts.py
RGB 16-bits : rgb-16bits.tif
XYZ 16-bits : xyz-16bits.tif
XYZ 16-bits (sans Gamma) : xyz-16bits-without-gamma.tif
RGB 8-bits : rgb-8bits.tif
XYZ 8-bits : xyz-8bits.tif
RGB 16-bits DCDM (12-bits dans du 16-bits) : rgb-16bits-DCDM.tif
4K RGB : 4096x2160.rgb.tif
4K XYZ (via ImageMagick) : 4096x2160.xyz.im.tif
4K XYZ (via Python) : 4096x2160.xyz.tif
Reference RGB-DCI-P3 Gamma 3 (2K) : reference_rgbdcip3_gamma26.tif
Reference sRGB (Gamma 2.2) reference_srgb.tif
Reference X'X'Z DCI Compliant (Gamma 2.6) reference_xyz.tif
Sortie du programme conversion_dcip3_to_xyz.py (X'Y'Z' DCI Compliant) : xyz-16bits.tif
SMPTE :
Autres ressources :
Divers ressources :
[4matrix] : Pour être honnête, nous avons 4 matrices, une pour "input sRGB -> output XYZ" et une autre pour "output XYZ -> input sRGB", et la même pour le RGB DCI-P3)
Certains espaces colorimétriques comme ceux développés par ARRI, Sony ou même Canon possèdent certaines de leurs primaires hors des limites et même avoir des valeurs négatives, mais cela reste des exceptions (peut-être pas pour longtemps) : 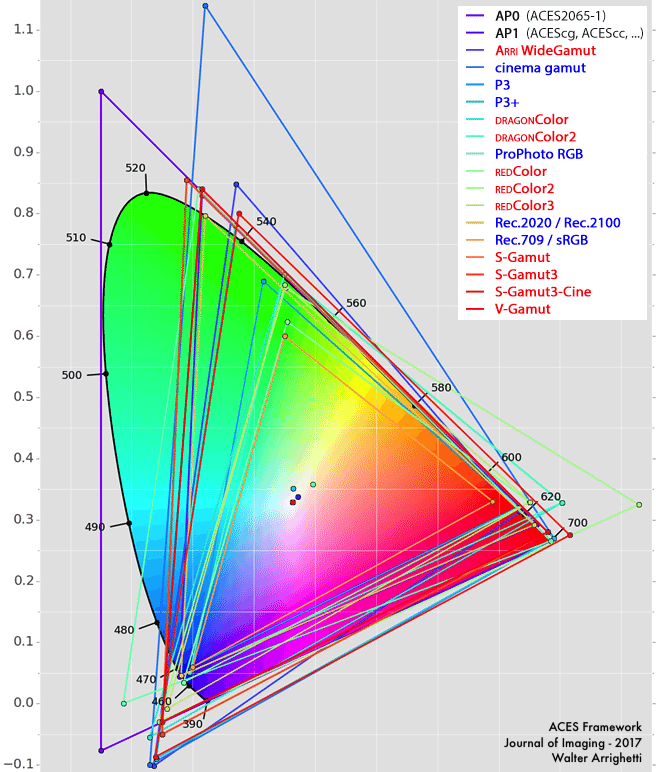 ↩
↩
Ce que représente concrètement le X, le Y et le Z : ↩
The XYZ color space is the original model developed by the CIE. The Y channel represents the luminance of a color. The Z channel approximately relates to the amount of blue in an image, but the value of Z in the XYZ color space is not identical to the value of B in the RGB color space. The X channel does not have a clear color analogy. However, if you consider the XYZ color space as a 3-D coordinate system, then X values lie along the axis that is orthogonal to the Y (luminance) axis and the Z axis. -- Understanding Color Spaces and Color Space Conversion
The CIE color model takes the luminance (as measure for perceived brightness) as one of the three color coordinates, calling it Y. The spectral response of the luminance is specified as the photopic luminosity function (..) The coordinate Z responds mostly to shorter-wavelength light, while X responds both to shorter-wavelength and longer-wavelength light. -- Color Spaces (Dr. Rüdiger Paschotta)
CIE XYZ functions are closely related to a linear transform of the LMS cone signals. L = long wavelength, M = middle wavelength, S = short wavelength. -- Fundamentals of Imaging Colour Spaces (Charles A. Wüthrich)
Transformation LMS→XYZ :
[ X ] [ 1.9102 ; -1.1121 ; 0.2019 ][L]
[ Y ] = [ 0.3710 ; 0.6291 ; 0.0000 ][M]
[ Z ] [ 0.0000 ; 0.0000 ; 1.0000 ][S]
Transformation XYZ→LMS :
[ L ] [ 0.3897 ; 0.6890 ; -0.0787 ][X]
[ M ] = [ -0.2298 ; 1.1834 ; 0.0464 ][Y]
[ S ] [ 0.0000 ; 0.0000 ; 1.0000 ][X]
Autre matrices : https://psychology.fandom.com/wiki/LMScolorspace
XYZ primaries are hypothetical because they do not correspond to any real light wavelengths. It is additive scheme color spaces, since it define the amounts of three stimuli provided to the eye (the three primaries). (...) XYZ system is based on the color matching experiments. X, Y and Z are extrapolations of RGB created mathematically to avoid negative numbers and are called Tristimulus values. X-value in this model represents approximately the red/green part of a color. Y-value represents approximately the lightness and the Z-value corresponds roughly to the blue/yellow part. -- CIE RGB and CIE XYZ Color Space
The X-value in this model represents approximately the red/green part of a color, the Y-value represents approximately the lightness and the Z-value corresponds roughly to the blue/yellow part. The X value accepts values from 0 to 95.047, the Y-value values from 0 to 100 and the Z-value values between 0 and 108.883. -- XYZ / CIE Color Spaces
In the XYZ color space, Y corresponds to relative luminance; Y also carries color information related to the eye's "M" (yellow-green) cone response. X and Z carry additional information about how the cones in the human eye respond to light waves of varying frequencies. -- Completely Painless Programmer's Guide to XYZ, RGB, ICC, xyY, and TRC
CIE (..) which established color spaces based on colors that can be perceived by the human eye. XYZ does not incorporate negative numbers and instead uses tristimulus values to define the color space that can be seen by the human eye. X represents the linear combination of the cone response non-negative curves created. Y represents luminance and Z is defined as almost equal to blue (blue/yellow) -- How to convert between sRGB and CIE XYZ
Theoretically, the XYZ color space has an infinite volume both in terms of colors and light -- SMPTE Journal, March 2018, Evaluation of Color Pixel Representations for High Dynamic Range Digital Cinema (Boitard, Jacquemin, Damberg, Stojmenovik, Ballestad) ↩
XYZ colorimetry is linear by definition, representing luminance levels that are proportional to the light on the screen. Linear light encoding is convenient for image synthesis and computer graphics because the underlying physics and shading models are linear. However, linear encoding does not match the response of the human visual system, which is approximately logarithmic in nature. -- Color and Mastering for Digital Cinema (Glenn Kennel) ↩
Les trois composantes X, Y et Z du modèle représentent respectivement la teinte, la luminance (intensité lumineuse pondérée par la sensibilité spectrale de l'œil) et la saturation. -- Anselme Brice & Gadal Sébastien ↩
Tristimulus: Intensités des trois couleurs imaginaires hors de la chromaticité possible, X, Y et Z, utilisées pour mesurer la luminance et la chromaticité ↩
A noter que cette matrice est pour le CIE 2-deg qui correspond à une référence de vision avec un angle de 2 degrès (il existe aussi CIE 10-deg, pour la vision périphérique) : ↩
Concernant la matrice 3x3 : ↩
La notation X'Y'Z' indique que le XYZ est accompagné de sa fonction de transfert qui est -normalement- que le Gamma. Cependant, dans certaines documentations, ils intègrent aussi la normalisation du point blanc et d'autres encore laissent supposer que la fonction de transfert englobe toute l'équation int( 4095( L * X / 52.37 ) (1/2.6) ), donc la normalisation du point blanc, le gamma et le bitdepth. ↩
Merci Rémi ;-) ↩