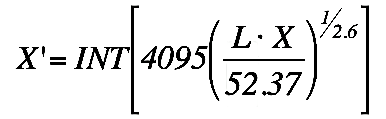
Une image dans le cinéma numérique n'est pas commune aux autres images que nous pouvons voir, elle respecte un certain workflow d'encodage, avec plusieurs processus pour aboutir à une image compatible cinéma numérique.
Ce workflow consiste à appliquer plusieurs transformations entre l'image d'origine jusqu'à avoir une image JPEG2000 XYZ et 12 bits.
Ce workflow est acté par deux équations mathématiques majeures :
|
|
|
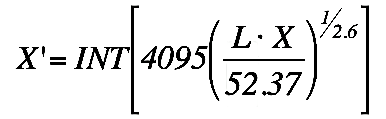
Ne vous enfuyez pas ! ... Revenez ! :)
Ces deux équations peuvent sembler complexes mais si elles sont prises morceau par morceau, elles ne se révèleront pas si difficiles à comprendre. Nous allons voir dans des chapitres séparés, chacune des parties :
| Conversion XYZ | Fonction de Transfert & Conversions |
|---|---|
|
|
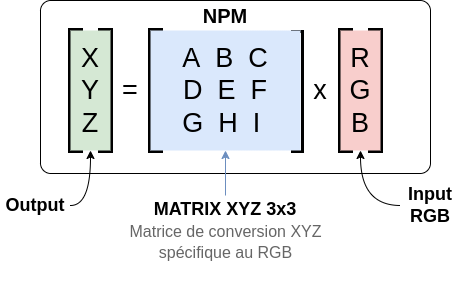
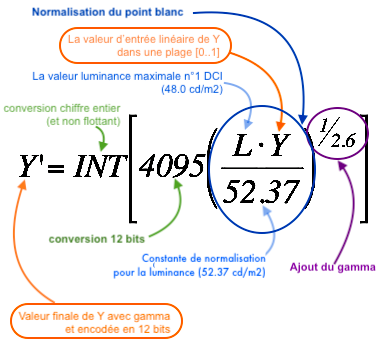
Prêt ? Allons-y ! :)
L'encodage d'une image pour le cinéma numérique doit respecter ces principes 1 :
Un exemple de workflow entre une image lambda et sa finalité en JPEG2000 X'Y'Z' / 12 bits par couleur :
Nous partons d'une image RGB en 16 bits par couleur par exemple : nous appliquons une transformation pour linéariser les données de l'image : cela consiste à supprimer son gamma pour avoir un gamma à 1. Nous appliquons notre transformation XYZ à l'aide de calcul matricielle pour avoir les données de l'image dans son nouvel espace colorimétrique XYZ, puis d'ajouter une petite normalisation du point blanc, l'ajout du gamma 3 et enfin une conversion en 12 bits.
A partir de là, nous pouvons intégrer notre image finale (notre JPEG2000 avec 12 bits par couleur, dans l'espace colorimétrique XYZ et avec un Gamma 2.6) dans notre MXF.
L'image du workflow ci-dessus est une représentation imagée (et simplifiée) de nos deux équations présentes en préambule, c'est tout de suite plus simple, non ? :)
Voir chapitre Linear pour de plus amples informations.
Voir chapitre XYZ pour de plus amples informations.
Voir chapitre White Point pour de plus amples informations.
Voir chapitre Gamma pour de plus amples informations.
Voir chapitre Bitdepth pour de plus amples informations.
A la fin de toutes ces conversions (XYZ et 12 bits), nous pouvons maintenant encoder notre image dans le format JPEG2000.
Voir chapitre JPEG2000.
En suivant ce workflow, vous venez d'avoir une image JPEG2000 conforme DCI/SMPTE.
Retrouvez tous les assets et programmes dans le répertoire assets/Image/
A partir de là, vous pouvez les intégrer dans votre MXF, notamment le MXF Picture.
SMPTE :
Ressources :
Les quelques références sur le workflow de conversion : ↩
Color conversion from R’G’B’ to X’Y’Z’ requires a three-step process which involves linearizing the color-corrected R’G’B’ signals (by applying a 2.6 gamma function), followed by their passage through a linear 3x3 transform matrix. The resultant linearized and coded XYZ signals are then given an inverse 2.6 gamma transfer characteristic whose output is quantized to 12 bits. -- SMPTE RP-431-2-2011 - DCinema Quality Reference Projector and Environement - Chapitre « Color Conversion to XYZ »
The digital files were linearized (applying a gamma of 2.6), then a 3x3 matrix was applied to convert RGB to XYZ, followed by application of the (1)/2.6 gamma function. The finished color-corrected files were stored as 12-bit X'Y'Z' data in 16-bit TIFF files. -- Color and Mastering for Digital Cinema (Glenn Kennel)
The DCI standard pixel representation specifies a quantization of the X’Y’Z’ color space using 12 bits and a 2.6 gamma power law TF with a peak luminance of 52.37 cd/m2 -- SMPTE Journal, March 2018, Evaluation of Color Pixel Representations for High Dynamic Range Digital Cinema (Boitard, Jacquemin, Damberg, Stojmenovik, Ballestad)
Qu'est-ce que veut dire le terme « Composant » ? Le terme composant peut être déroutant la première fois, mais c'est une autre façon de dire "couleur"... mais pas totalement ;-) ↩
Dans un système RGB, on peut dire qu'on a 3 couleurs - rouge, vert et bleu - donc 3 composants.
Mais alors pourquoi dire "3 composants" au lieu de "3 couleurs" : tout simplement parce que dans d'autres systèmes colorimétriques - et notamment avec le XYZ - ne sont pas des couleurs que représentent le X, le Y ou le Z, mais ce sont des valeurs qui - avec des calculs spécifiques - permettent de stocker certaines informations précises.
Par exemple, avec le XYZ, le Y ne désigne pas une couleur mais désigne la valeur de la luminance.
Imaginez juste un composant comme un emplacement de stockage pour une donnée. Cette donnée peut être une valeur de couleur (R,G ou B) ou une valeur autre comme le Y du XYZ.
Pour des raisons de simplicité et de compréhension, il peut m'arriver d'utiliser le terme "couleur" au lieu de "composant", mais c'est un léger abus de langage pour les besoins de la documentation.
Sur le schéma, il est indiqué que seul le Gamma appartient à la fonction de transfert (function transfer). Dans d'autres documentations, ils intègrent aussi la normalisation du point blanc et d'autres encore laisse supposer que la fonction de transfert englobe toute l'équation int( 4095 ( L*X / 52.37 ) 1 / 2.6 ), donc la normalisation du point blanc, le gamma et le bitdepth. ↩